
前項までですべての準備が整い,\ 本項から本題の「統計的な推測」に入る.
これまでは,\ 母集団の情報(既知)を元に,\ 未知の標本について考察してきた.
例えば,\ 母平均が$m$であるとき,\ 標本平均の期待値も$E( X)=m$となるのであった.
しかし,\ 実用上は,\ 母集団が未知で,\ しかも全数調査が困難であることが多い.
標本を抽出してその情報を得て,\ それを元に母集団の情報(未知)を推定することになる.
例として,\ 全国の高校生男子の身長の平均が知りたいとしよう.
150万人ほどいる高校生男子の全数調査は,\ 時間的にも労力的にも合理性を欠く.
そこで,\ 無作為に100人を抽出して身長を測定すると,\ その標本平均が$ X$cmであった.
このとき,\ 全国の高校生男子の身長の平均(母平均$m$)は何cm位と推定できるだろうか.
100人は大きいから,\ 大数の法則より,\ 母平均$m}$は標本平均$ X}$に近い値である確率が高い.}
それでも,\ 全数調査なくして厳密に母平均を求めることはできず,\ 区間推定することになる.
しかし,\ どんな$a$であれ,\ 「絶対に$ X-a≦ m≦ X+a$\,」と言い切ることは難しい.
低い確率ながら偶然に母平均$m$とかけ離れた100人が抽出される可能性もあるからである.
結局,\,どの程度信頼できるかを確率で表した区間$ X-a≦ m≦ X+a}$を求めることになる.}
確率大かつ誤差小が理想だが,\ 誤差と確率はトレードオフの関係にあるので両立できない.}
例えば,\ 「信頼度99.99\%で$166≦ m≦174$」では区間が広すぎて実用性が低い.
一方で,\ 「信頼度50\%で$169.7≦ m≦170.3$」では確率が低すぎて信頼できない.
そこで,\ 信頼度を95\%として誤差と確率のバランスをとることが多い.}
「信頼度95\%で$169≦ m≦171$」ならば有用性が感じられるのではないだろうか.
95に明確な数学的根拠はないので,\ 目的や状況によって何\%にするかを決めればよい.
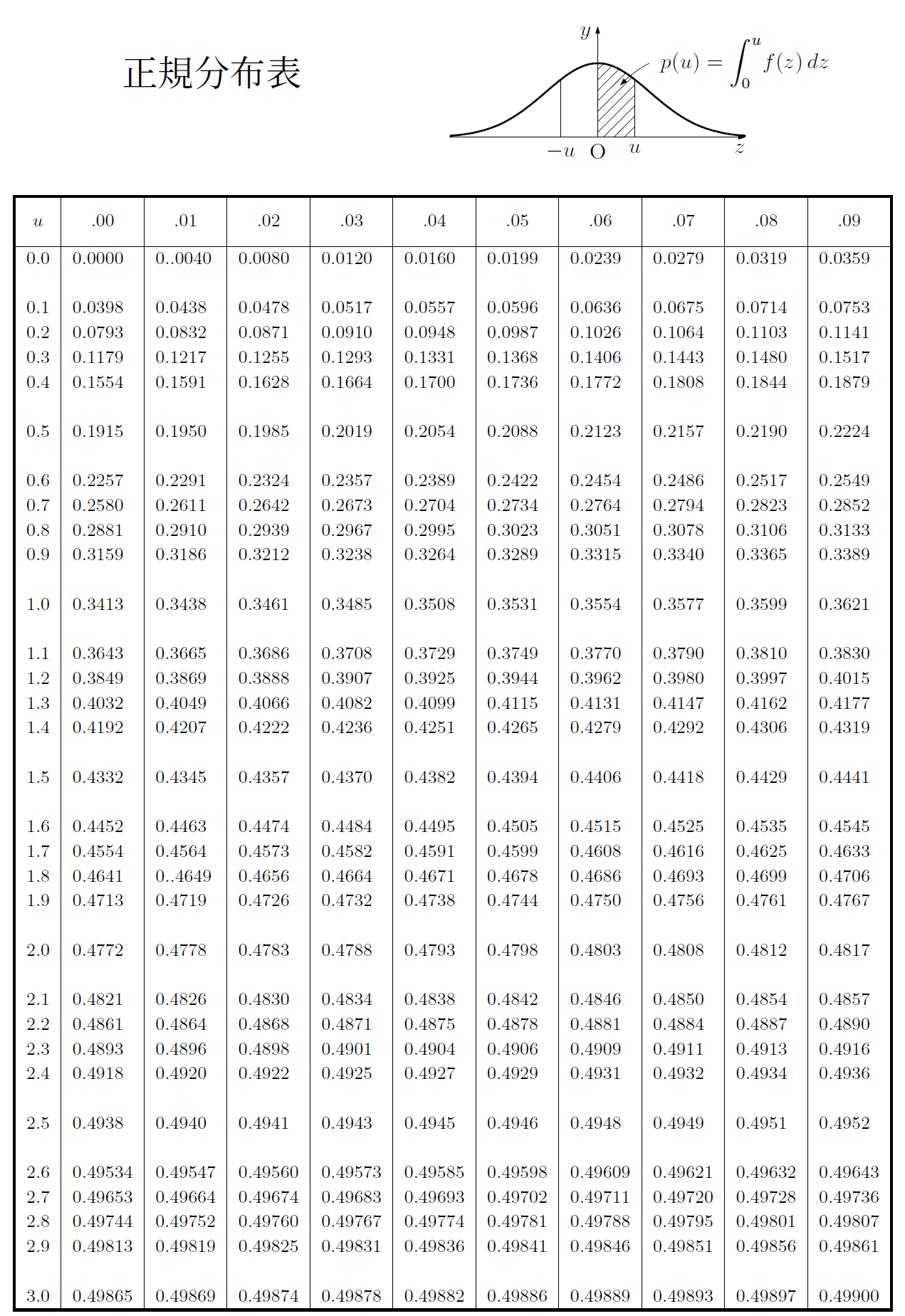
標本の大きさ$n$が大きいとき,\ $ X$は近似的に正規分布$N-.2zw}m,\ σ^2}{n}$に従う(中心極限定理).
よって,\ $Z= X-m}{σ}{√ n$は近似的に標準正規分布$N(0,\ 1)$に従う. \\
この$m$の区間を母平均$m$に対する信頼度95\%の信頼区間といい,
信頼度は99\%で考えることも多く,\ 同様に計算すると1.96ではなく2.58となる. \\
母平均$m}$の推定
$m$に対する\信頼度95\%の信頼区間
※\ \ $ X:標本平均,\ \ n:標本の大きさ$,\ \ $σ :母標準偏差$
※\ \ $n}$が大きいとき,\ 母標準偏差$σ}$を標本標準偏差$S}$で代用してよい.全国の高校生男子の中から無作為に100人を抽出して身長を測定したところ,\ その平均
は170\,cm,\ 標準偏差は5\,cmであった.\ 全国の高校生男子の平均身長を信頼度95\%と
信頼度99\%で推定せよ.\ また,\ 信頼度95\%の信頼区間の幅を1cm以下にするには最低 \\
信頼区間を公式として暗記しておき,\ 代入するだけである.
ただし,\ 本問では母標準偏差\,σ\,が不明なので,\ 標本標準偏差S=5で代用する.}
信頼区間の幅1.96×σ}{√ n}×2を\,1}{10}\,にしたければ,\ nを100倍にする必要がある.
また,\ 母標準偏差\,σ\,は一定値なので,\ 同じnに対しては信頼区間の幅1.96×σ}{√ n}×2も一定である.
しかし,\ 標本標準偏差Sは標本の選び方次第で変わる確率変数}である.
よって,\ σ\,をSで代用する場合,\ 標本の選び方次第で信頼区間の幅1.96×S}{√ n}×2も変わる.}
さて,\ 信頼区間はその意味合いを誤解しやすい}ので注意しなければならない.
上の問題で,\ 信頼度95\%の信頼区間が$[\,169.02,\ 170.98\,]$と求まった.
これを次のように解釈するのは重大な誤りである.確率で変化する母平均$m$は,\ 95\%の確率で1つの区間$[\,169.02,\ 170.98\,]$内の値をとる. 母平均$m}$は母集団によって決まる定数であり,\ 確率で変化したりはしない.確率で変化するのは標本平均$ X}$,\ つまりは信頼区間の方である.
結局,\ 信頼度95\%の信頼区間の正しい解釈は次となる. 標本を抽出して信頼区間を求めることを100回繰り返す. このとき,\ 母平均$m}$を含む信頼区間が95個程度できる.150万人から100人を抽出する方法は$C{150万}{100}$通り. 全てに対して信頼区間がそれぞれ求まり,\ それらの95\%が母平均$m$を含んでいる. [\,169.02,\ 170.98\,]$は信頼区間の1つを求めたにすぎない. これが$m$を含む信頼区間(全体の95\%)の1つなのか含まない信頼区間(全体の5\%)の1つなのかは神のみぞ知るが, 全数調査をして母平均$m$を求めたならばわかる

