自分でスライダーを動かすこともできますし、左下には自動再生ボタンがあります。右上は初期状態へのリセットボタンです。
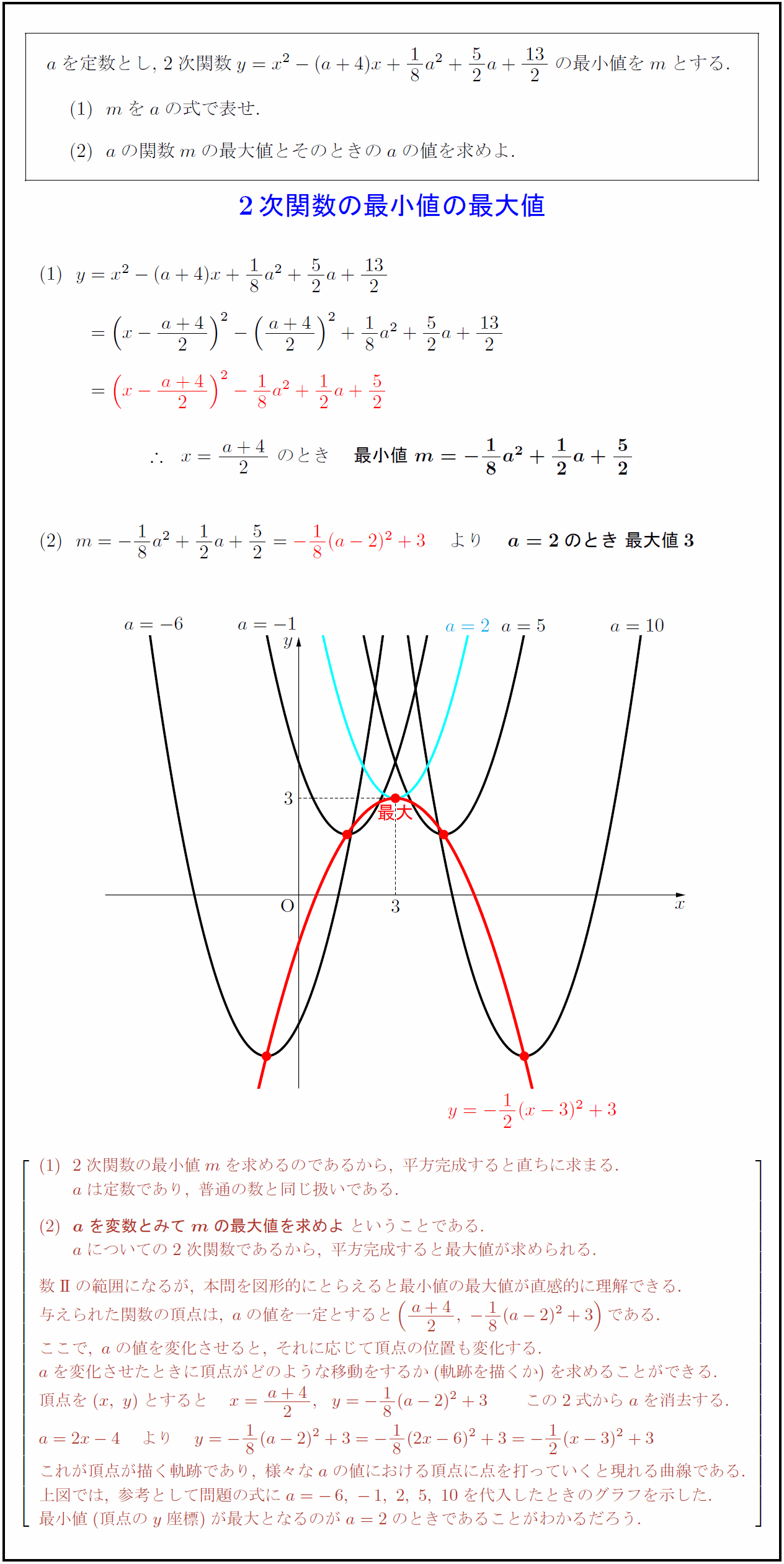
a$を定数とし,\ 2次関数$y=x²-(a+4)x+18a²+52a+{13}{2}$の最小値を$m$とする. $m$を$a$の式で表せ. $a$の関数$m$の最大値とそのときの$a$の値を求めよ. 2次関数の最小値の最大値} 2次関数の最小値mを求めるのであるから,\ 平方完成すると直ちに求まる. aは定数であり,\ 普通の数と同じ扱いである. {aを変数とみてmの最大値を求めよ}ということである. aについての2次関数であるから,\ 平方完成すると最大値が求められる. 数II}の範囲になるが,\ 本問を図形的にとらえると最小値の最大値が直感的に理解できる. 与えられた関数の頂点は,\ aの値を一定とすると({a+4}{2},\ -18(a-2)²+3)である. ここで,\ aの値を変化させると,\ それに応じて頂点の位置も変化する. aを変化させたときに頂点がどのような移動をするか(軌跡を描くか)を求めることができる. 頂点を(x,\ y)とすると x={a+4}{2},y=-18(a-2)²+3 この2式からaを消去する. a=2x-4 より y=-18(a-2)²+3=-18(2x-6)²+3=-12(x-3)²+3 これが頂点が描く軌跡であり,\ 様々なaの値における頂点に点を打っていくと現れる曲線である. 上図では,\ 参考として問題の式にa=-6,\ -1,\ 2,\ 5,\ 10を代入したときのグラフを示した. 最小値(頂点のy座標)が最大となるのがa=2のときであることがわかるだろう.

