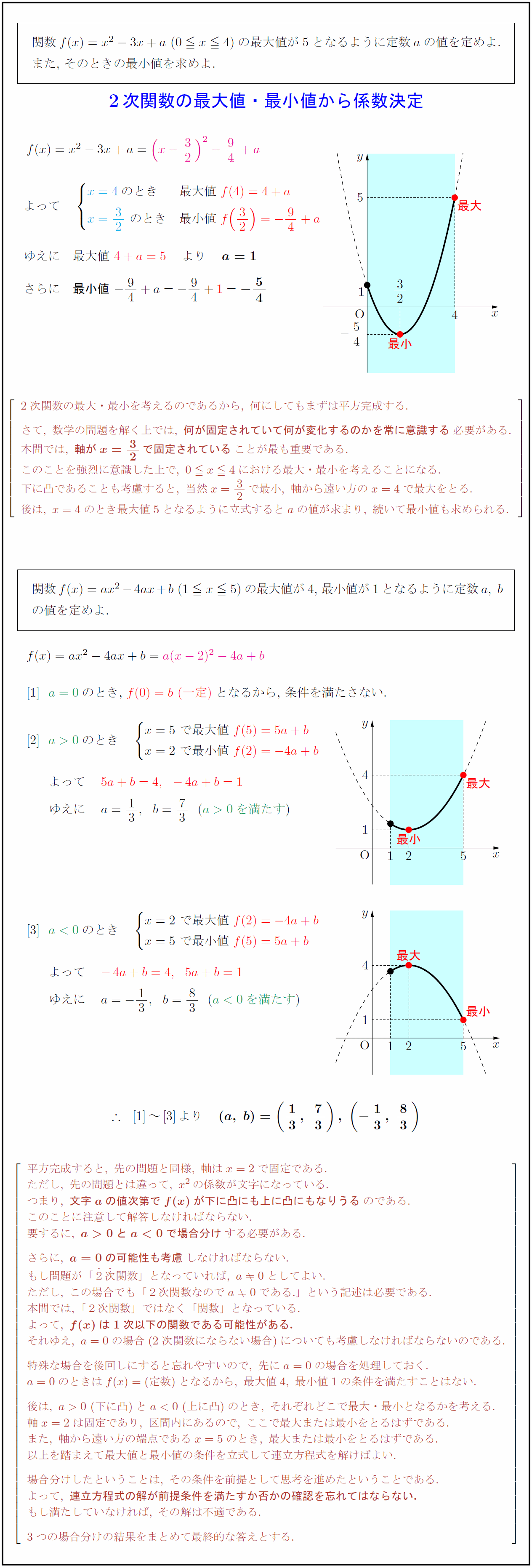
関数$f(x)=x²-3x+a\ (0 x4)$の最大値が5となるように定数$a$の値を定めよ. また,\ そのときの最小値を求めよ. 2次関数の最大値・最小値から係数決定 2次関数の最大・最小を考えるのであるから,\ 何にしてもまずは平方完成する. さて,\ 数学の問題を解く上では,\ {何が固定されていて何が変化するのかを常に意識する}必要がある. 本問では,\ {軸がx=32で固定されている}ことが最も重要である. このことを強烈に意識した上で,\ 0 x4における最大・最小を考えることになる. 下に凸であることも考慮すると,\ 当然x=32で最小,\ 軸から遠い方のx=4で最大をとる. 後は,\ x=4のとき最大値5となるように立式するとaの値が求まり,\ 続いて最小値も求められる. 関数$f(x)=ax²-4ax+b\ (1 x5)$の最大値が4,\ 最小値が1となるように定数$a,\ b$ の値を定めよ. {f(0)=b\ (一定)}$となるから,\ 条件を満たさない. 平方完成すると,\ 先の問題と同様,\ 軸はx=2で固定である. ただし,\ 先の問題とは違って,\ x²の係数が文字になっている. つまり,\ {文字aの値次第でf(x)が下に凸にも上に凸にもなりうる}のである. このことに注意して解答しなければならない. 要するに,\ {a>0とa<0で場合分け}する必要がある. さらに,\ {a=0の可能性も考慮}しなければならない. もし問題が「2}次}関数」となっていれば,\ a0としてよい. ただし,\ この場合でも「2次関数なのでa0である.」という記述は必要である. 本問では,\ 「2次関数」ではなく「関数」となっている. よって,\ {f(x)は1次以下の関数である可能性がある.} それゆえ,\ a=0の場合(2次関数にならない場合)についても考慮しなければならないのである. 特殊な場合を後回しにすると忘れやすいので,\ 先にa=0の場合を処理しておく. a=0のときはf(x)=(定数)となるから,\ 最大値4,\ 最小値1の条件を満たすことはない. 後は,\ a>0\ (下に凸)とa<0\ (上に凸)のとき,\ それぞれどこで最大・最小となるかを考える. 軸x=2は固定であり,\ 区間内にあるので,\ ここで最大または最小をとるはずである. また,\ 軸から遠い方の端点であるx=5のとき,\ 最大または最小をとるはずである. 以上を踏まえて最大値と最小値の条件を立式して連立方程式を解けばよい. 場合分けしたということは,\ その条件を前提として思考を進めたということである. よって,\ {連立方程式の解が前提条件を満たすか否かの確認を忘れてはならない.} もし満たしていなければ,\ その解は不適である. 3つの場合分けの結果をまとめて最終的な答えとする.

