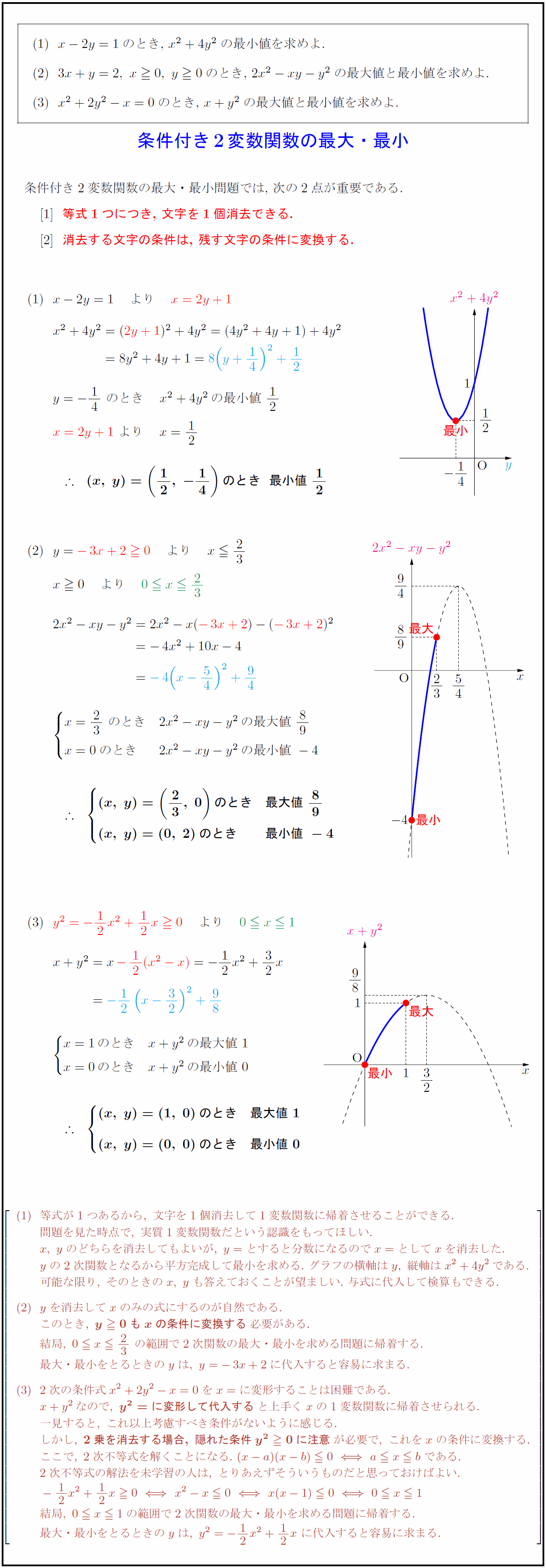
条件付き2変数関数の最大・最小問題では,\ 次の2点が重要である. 等式1つにつき,\ 文字を1個消去できる. 消去する文字の条件は,\ 残す文字の条件に変換する.} 等式が1つあるから,\ 文字を1個消去して1変数関数に帰着させることができる. 問題を見た時点で,\ 実質1変数関数だという認識をもってほしい. x,\ yのどちらを消去してもよいが,\ y=とすると分数になるのでx=としてxを消去した. yの2次関数となるから平方完成して最小を求める.\ グラフの横軸はy,\ 縦軸はx²+4y²である. 可能な限り,\ そのときのx,\ yも答えておくことが望ましい.\ 与式に代入して検算もできる. yを消去してxのみの式にするのが自然である. このとき,\ {y0もxの条件に変換する}必要がある. 結局,\ 0 x23\ の範囲で2次関数の最大・最小を求める問題に帰着する. 最大・最小をとるときのyは,\ y=-3x+2に代入すると容易に求まる. 2次の条件式x²+2y²-x=0をx=に変形することは困難である. x+y²なので,\ {y²=に変形して代入する}と上手くxの1変数関数に帰着させられる. 一見すると,\ これ以上考慮すべき条件がないように感じる. しかし,\ {2乗を消去する場合,\ 隠れた条件y²0に注意}が必要で,\ これをxの条件に変換する. ここで,\ 2次不等式を解くことになる.(x-a)(x-b)0a x bである. 2次不等式の解法を未学習の人は,\ とりあえずそういうものだと思っておいてほしい. -12x²+12x0x²-x0x(x-1)00 x1 結局,\ 0 x1の範囲で2次関数の最大・最小を求める問題に帰着する. 最大・最小をとるときのyは,\ y²=-12x²+12x\ に代入すると容易に求まる.

