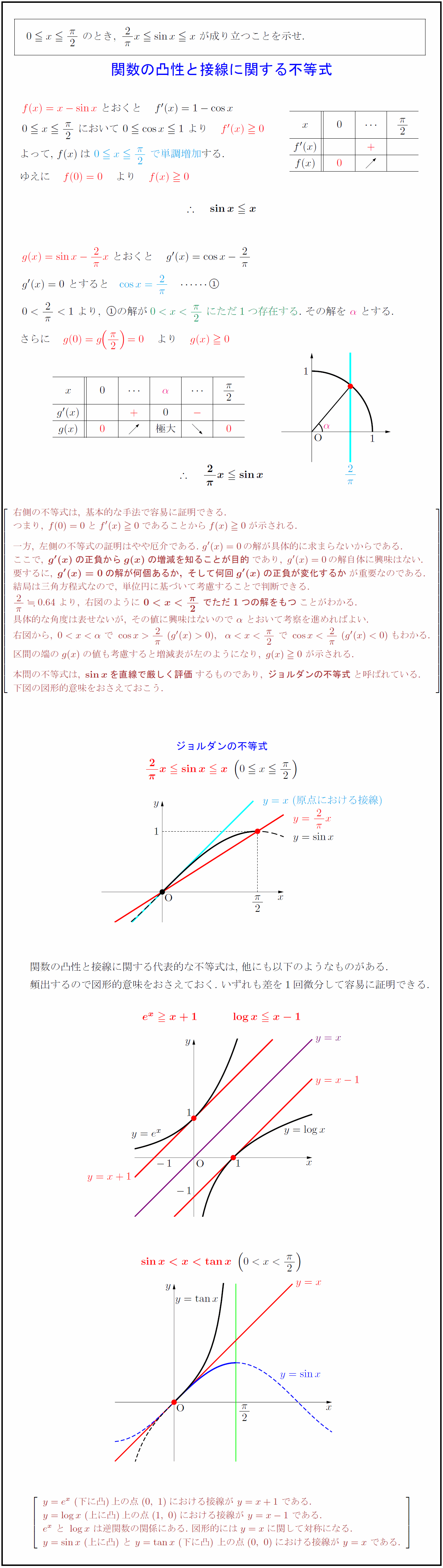
右側の不等式は,\ 基本的な手法で容易に証明できる. つまり,\ f(0)=0とf'(x)0であることからf(x)0が示される. 一方,\ 左側の不等式の証明はやや厄介である.\ g'(x)=0の解が具体的に求まらないからである. ここで,\ {g'(x)の正負からg(x)の増減を知ることが目的}であり,\ g'(x)=0の解自体に興味はない. 要するに,\ {g'(x)=0の解が何個あるか,\ そして何回g'(x)の正負が変化するか}が重要なのである. 結局は三角方程式なので,\ 単位円に基づいて考慮することで判断できる. {2}{π}0.64\ より,\ 右図のように\ {0<x<{π}{2}\ でただ1つの解をもつ}ことがわかる. 具体的な角度は表せないが,\ その値に興味はないので\ α\ とおいて考察を進めればよい. 右図から,\ 0<x<α\ で\ cos x>{2}{π}\ (g'(x)>0),α<x<{π}{2}\ で\ cosx<{2}{π}\ (g'(x)<0)もわかる. 区間の端のg(x)の値も考慮すると増減表が左のようになり,\ g(x)0\ が示される. \本問の不等式は,\ {sin xを直線で厳しく評価}するものであり,\ {ジョルダンの不等式}と呼ばれている. 下図の図形的意味をおさえておこう.ジョルダンの不等式} 関数の凸性と接線に関する代表的な不等式は,\ 他にも以下のようなものがある. 頻出するので図形的意味をおさえておく.\ いずれも差を1回微分して容易に証明できる. y=e^x\ (下に凸)上の点(0,\ 1)における接線が\ y=x+1\ である. y=log x\ (上に凸)上の点(1,\ 0)における接線が\ y=x-1\ である. e^x\ と\ log x\ は逆関数の関係にある.\ 図形的にはy=xに関して対称になる. y=sin x\ (上に凸)\ と\ y=tan x\ (下に凸)\ 上の点(0,\ 0)における接線が\ y=x\ であ

