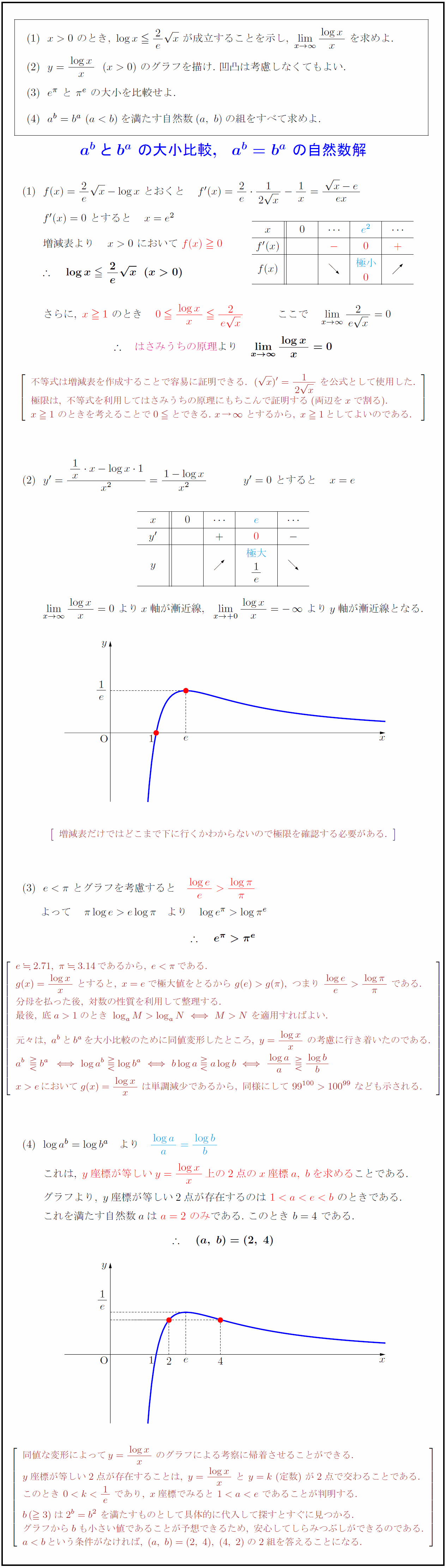
x>0\ のとき,\ log x2e x\ が成立することを示し,\ lim[x→∞]{log x}{x}\ を求めよ.$ $y={log x}{x}(x>0)\ のグラフを描け.\ 凹凸は考慮しなくてもよい.$ $e^π\ と\ π^e\ の大小を比較せよ $a^b=b^a\ (ag(π),\ つまり\ {log e}{e}>{log π}{π}\ である. 分母を払った後,\ 対数の性質を利用して整理する. 最後,\ 底a>1のとき\ log_aM>log_aNM>N\ を適用すればよい. 元々は,\ a^bとb^aを大小比較のために同値変形したところ,\ y={log x}{x}\ の考慮に行き着いたのである. x>eにおいてg(x)={log x}{x}\ は単調減少であるから,\ 同様にして\ 99^{100}>100^{99}\ なども示される. $これは,\ y座標が等しいy={log x}{x}上の2点のx座標a,\ bを求める}ことである.$ $グラフより,\ y座標が等しい2点が存在するのは\ 1

