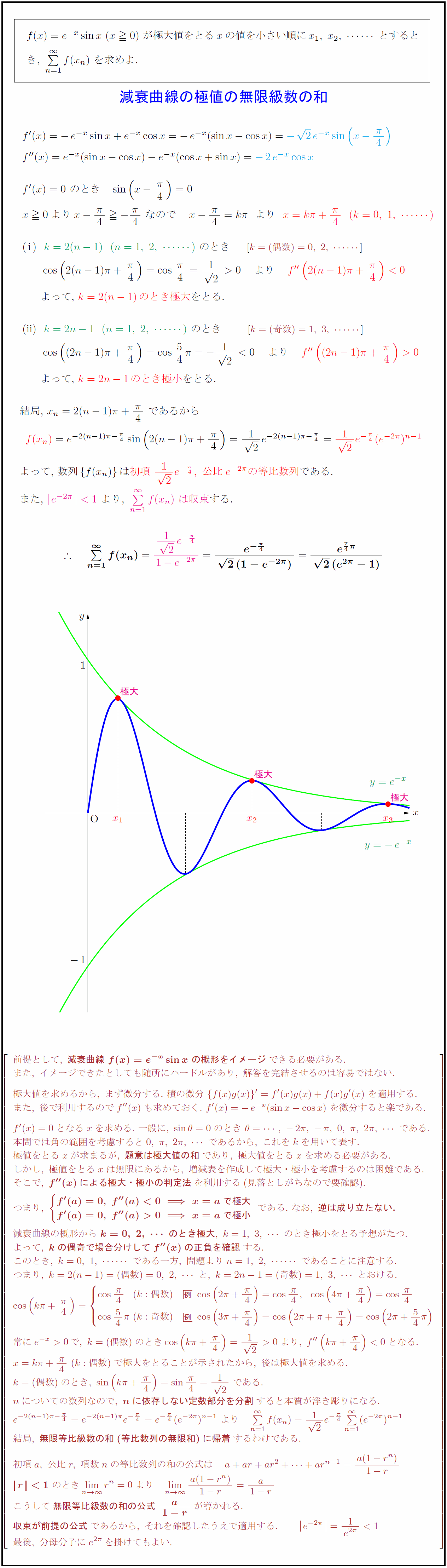
f(x)=e^{-x}sin x\ (x0)\ が極大値をとるxの値を小さい順にx₁,\ x₂,とすると$ $き,\ Σf(x_n)\ を求めよ.$ よって,\ $k=2(n-1)のとき極大}をとる.$ よって,\ $数列f(x_n)}は初項\ {1}{2}e^{-π/4,\ 公比e^{-2π}の等比数列}である.$ また,\ $e^{-2π<1}\ より,\ Σf(x_n)\ は収束}する.$ 前提として,\ {減衰曲線\ f(x)=e^{-x}sin x\ の概形をイメージ}できる必要がある. また,\ イメージできたとしても随所にハードルがあり,\ 解答を完結させるのは容易ではない. 極大値を求めるから,\ まず微分する.\ 積の微分\ {f(x)g(x)}'=f'(x)g(x)+f(x)g'(x)\ を適用する. また,\ 後で利用するのでf''(x)も求めておく.\ f'(x)=-e^{-x}(sin x-cos x)\ を微分すると楽である. f'(x)=0となるxを求める.\ 一般に,\ sinθ=0 のとき\ θ=,\ -2π,\ -π,\ 0,\ π,\ 2π,である. 本問では角の範囲を考慮すると0,\ π,\ 2π,であるから,\ これをkを用いて表す. 極値をとるxが求まるが,\ {題意は極大値の和}であり,\ 極大値をとるxを求める必要がある. しかし,\ 極値をとるxは無限にあるから,\ 増減表を作成して極大・極小を考慮するのは困難である. そこで,\ {f''(x)による極大・極小の判定法}を利用する(見落としがちなので要確認). である.\ なお,\ {逆は成り立たない.} [-.7zh] 減衰曲線の概形から\ {k=0,\ 2,のとき極大},\ k=1,\ 3,のとき極小をとる予想がたつ. よって,\ {kの偶奇で場合分けしてf''(x)の正負を確認}する. このとき,\ k=0,\ 1,である一方,\ 問題よりn=1,\ 2,であることに注意する. つまり,\ k=2(n-1)=(偶数)=0,\ 2,と,\ k=2n-1=(奇数)=1,\ 3,とおける. x=kπ+{π}{4}\ (k:偶数)で極大をとることが示されたから,\ 後は極大値を求める. k=(偶数)のとき,\ sin(kπ+{π}{4})=sin{π}{4}={1}{2}\ である. nについての数列なので,\ {nに依存しない定数部分を分割}すると本質が浮き彫りになる. 結局,\ {無限等比級数の和(等比数列の無限和)に帰着}するわけである. 初項a,\ 公比r,\ 項数nの等比数列の和 こうして{無限等比級数の和の公式\ {a}{1-r\ が導かれる. {収束が前提の公式}であるから,\ それを確認したうえで適用する. e^{-2π={1}{e^{2π

