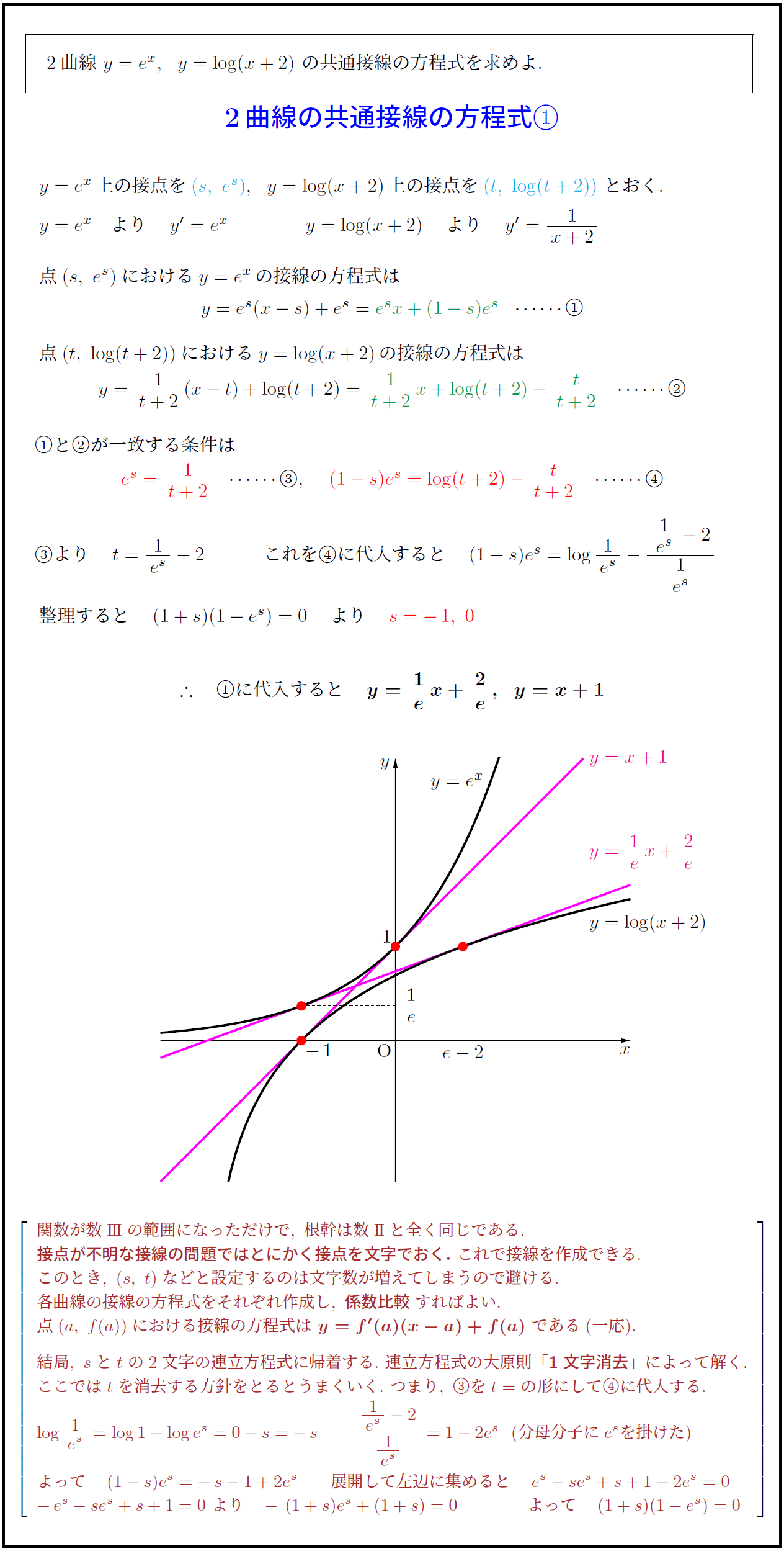
2曲線\ y=e^x,y=log(x+2)\ の共通接線の方程式を求めよ. $y=e^x上の接点を(s,\ e^s)},y=log(x+2)上の接点を(t,\ log(t+2))}\ とおく.$ $y=e^x より y’=e^x y=log(x+2) より y’={1}{x+2}$ $点(s,\ e^s)におけるy=e^xの接線の方程式は$ $点(t,\ log(t+2))におけるy=log(x+2)の接線の方程式は$ とが一致する条件は $整理すると (1+s)(1-e^s)=0 より s=-1,\ 0}$ 関数が数III}の範囲になっただけで,\ 根幹は数II}と全く同じである. {接点が不明な接線の問題ではとにかく接点を文字でおく.}\ これで接線を作成できる. このとき,\ (s,\ t)などと設定するのは文字数が増えてしまうので避ける. 各曲線の接線の方程式をそれぞれ作成し,\ {係数比較}すればよい. 点(a,\ f(a))における接線の方程式は\ {y=f'(a)(x-a)+f(a)}\ である(一応). 結局,\ sとtの2文字の連立方程式に帰着する.\ 連立方程式の大原則「{1文字消去}」によって解く. ここではtを消去する方針をとるとうまくいく.\ つまり,\ をt=の形にしてに代入する. -log{1}{e^s}=-(log1-log e^s)=-(0-s)=s 1}{e^s}-2}1}{e^s=1-2e^s(分母分子にe^sを掛けた) よって (1-s)e^s=-s-1+2e^s 展開して左辺に集めると e^s-se^s+s+1-2e^s=0 ゆえに -e^s-se^s+s+1=0 より -(1+s)e^s+(1+s)=0

