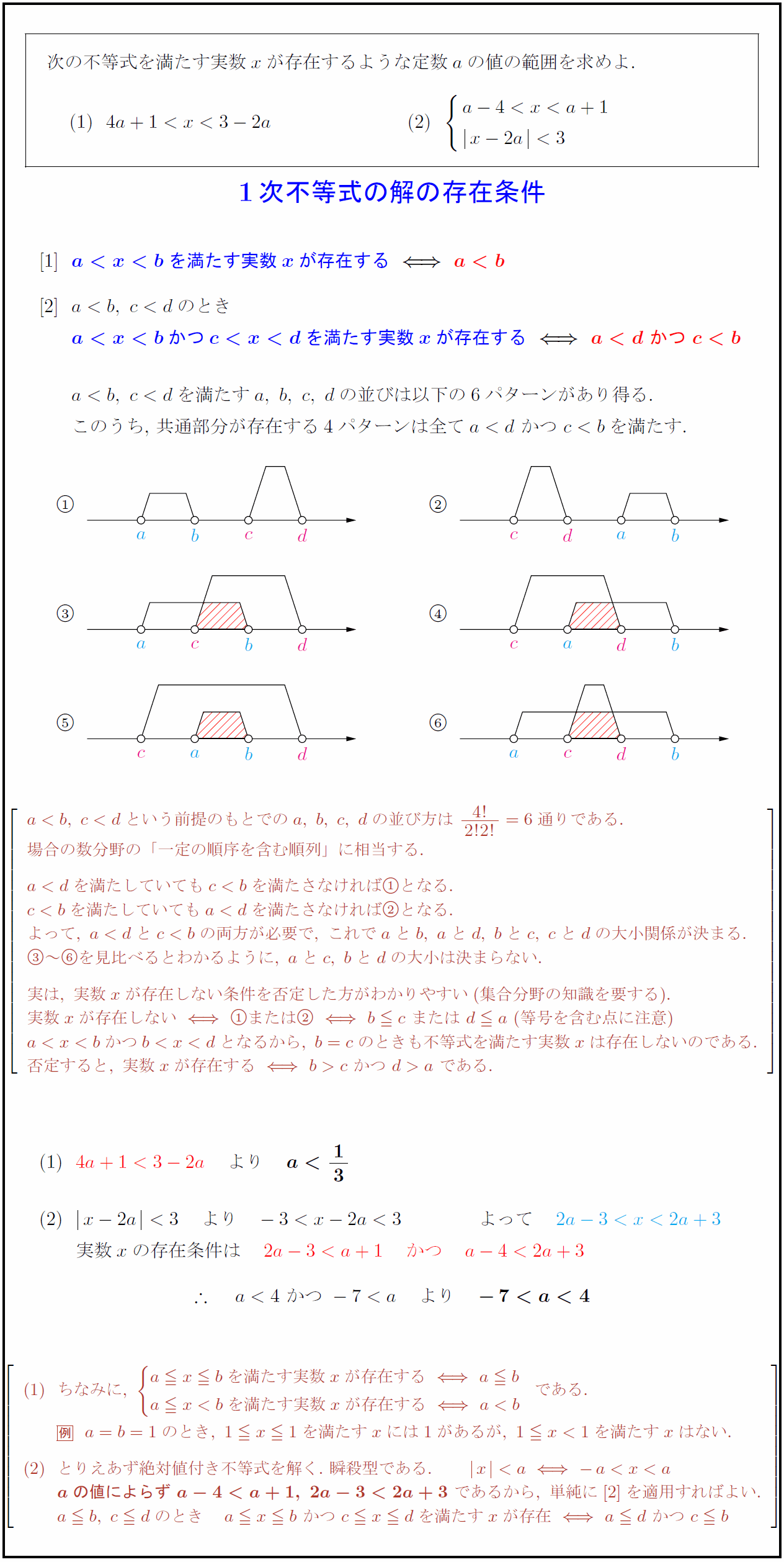
次の不等式を満たす実数$x$が存在するような定数$a$の値の範囲を求めよ.{1次不等式の解の存在条件を満たす実数xが存在する}\を満たす実数xが存在する}\ を満たす$a,\ b,\ c,\ d$の並びは以下の6パターンがあり得る. { }このうち,\ 共通部分が存在する4パターンは全て$を満たす.という前提のもとでのa,\ b,\ c,\ dの並び方は\ {4!}{2!2!}=6通りである. 場合の数分野の「一定の順序を含む順列」に相当する. を満たしていてもを満たさなければとなる. を満たしていてもを満たさなければとなる. よって,\ の両方が必要で,\ これでaとb,\ aとd,\ bとc,\ cとdの大小関係が決まる. ~⑥を見比べるとわかるように,\ aとc,\ bとdの大小は決まらない. 実は,\ 実数xが存在しない条件を否定した方がわかりやすい(集合分野の知識を要する). 実数xが存在しないまたはb c\ または\ d a\ (等号を含む点に注意) となるから,\ b=cのときも不等式を満たす実数xは存在しないのである. 否定すると,\ 実数xが存在するである. }]$ $4a+13-2a} より {a13}$ $x-2a} { }$実数xの存在条件は $[l} ちなみに,\ a x bを満たす実数xが存在するa b a x< bを満たす実数xが存在するa

