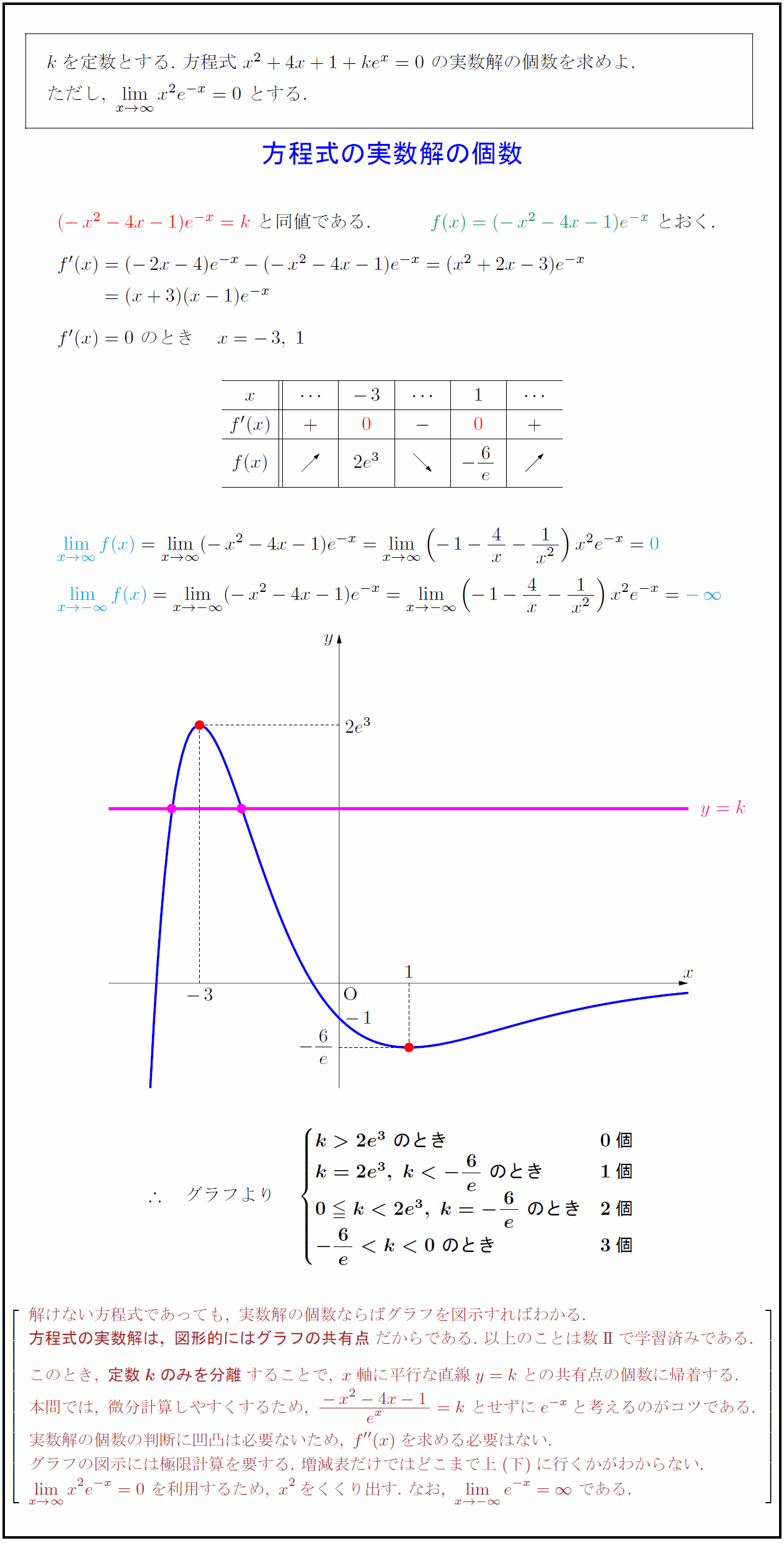
kを定数とする.\ 方程式\ x²+4x+1+ke^x=0\ の実数解の個数を求めよ.$ 同値である 解けない方程式であっても,\ 実数解の個数ならばグラフを図示すればわかる. {方程式の実数解は,\ 図形的にはグラフの共有点}だからである.\ 以上のことは数II}で学習済みである. このとき,\ {定数kのみを分離}することで,\ x軸に平行な直線y=kとの共有点の個数に帰着する. 本問では,\ 微分計算しやすくするため,\ {-x²-4x-1}{e^x}=k\ とせずにe^{-x}と考えるのがコツである. 実数解の個数の判断に凹凸は必要ないため,\ f”(x)を求める必要はない. グラフの図示には極限計算を要する.\ 増減表だけではどこまで上(下)に行くかがわからない. lim[x→∞]x²e^{-x}=0\ を利用するため,\ x²をくくり出す.\ なお,\ limx→-∞}e^{-x}=-∞\ である.

