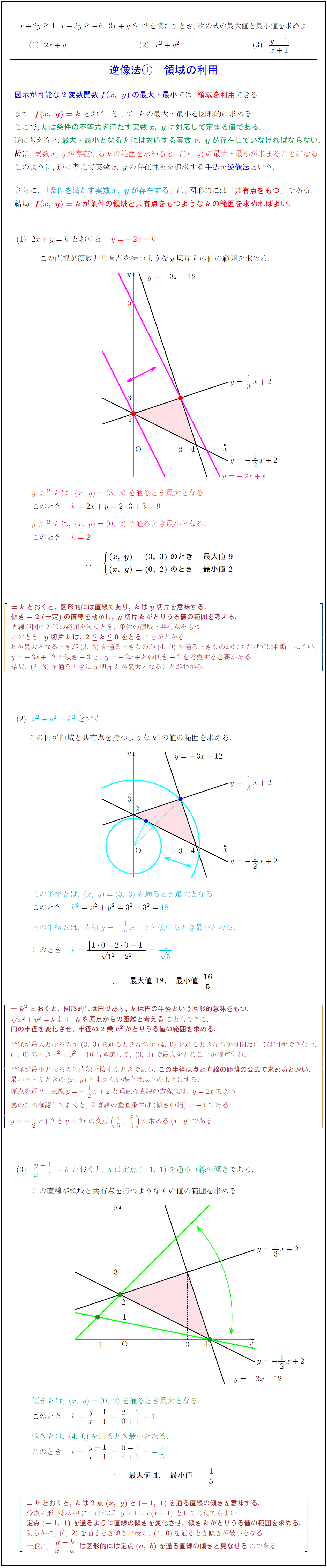
図示が可能な2変数関数${f(x,\ y)}$の最大・最小では,\ 領域を利用できる. ${f(x,\ y)=k\ とおくと,\ {条件を満たす実数x,\ yに対応してkが定まる.$ 逆に考えると,\ ${kには対応する実数x,\ yが必ず存在がしているはずである.$ このことを利用して,\ $kの範囲を定めることができる.$ 「条件を満たす実数${x,\ y}$が存在する}」は,\ 図形的には「共有点をもつ}」だ.} 要は,\ ${f(x,\ y)=kが条件の領域と共有点をもつようにkの範囲を定める.$ このように,\ 逆に考えて実数$x,\ y$の存在を追求する手法を逆像法という. この直線が領域と共有点を持つようなkの値の範囲を求める.$ {=k\ とおくと,\ 図形的には直線であり,\ kはy切片を意味する.} {直線の傾き-2\ (一定)で変化させ,\ y切片kがとりうる値の範囲を求める.} 直線が図の矢印の範囲を動くとき,\ 条件の領域と共有点をもつ. このとき,\ {y切片kは,\ 2 k9\ をとる}ことがわかる. (3,\ 3)を通るときと(4,\ 0)を通るときがシビアなのでよく注意して判断する. y=-3x+12の傾き-3と,\ y=-2x+kの傾き-2を考慮する必要がある. 結局,\ (3,\ 3)を通るとき,\ y切片kが最大となることがわかる. { }\ $この円が領域と共有点を持つようなk²の値の範囲を求める.$ 円の半径kは,\ (x,\ y)=(3,\ 3)を通るとき最大となる.}円の半径kは,\ 直線y=-12x+2と接するとき最小となる.}$ {=k²\ とおくと,\ 図形的には円であり,\ kは円の半径を意味する.} {円の半径を変化させ,\ 半径の2乗k²がとりうる値の範囲を求める.} 最大となるのが,\ (3,\ 3)を通るときか(4,\ 0)を通るときかは微妙である. 4²+0²=16も計算して比較した上で,\ 解答を作成することになる. 最小となるのは,\ 直線と接するときなので,\ {半径を点と直線の距離の公式で求める.} kは定点(-1,\ 1)を通る直線の傾き}であるこの直線が領域と共有点を持つようなkの値の範囲を求める.$ 傾きkは,\ (x,\ y)=(0,\ 2)を通るとき最大となる.}$ { }\ $傾きkは,\ (4,\ 0)を通るとき最小となる.}$ {=k\ とおくと,\ 図形的には定点を通る直線で,\ kは直線の傾きを意味する.} 分数の形がわかりにくければ,\ y-1=k(x+1)\ と考えてもよい. {定点(-1,\ 1)を通るよう直線の傾きを変化させ,\ kがとりうる値の範囲を求める.} (0,\ 2)を通るとき最大,\ (4,\ 0)を通るとき最小であることがすぐにわかるだろう. 一般に,\ y-b}{x-a}\ は,\ 図形的には定点(a,\ b)を通る直線の傾きと見なせる}のだ. { }\ $kは定点(2,\ -2)を通る直線の傾きである.$ { }\ $直線が円と共有点を持つようなkの値の範囲を求める.$ $ {最大値\ 1, 最小値\ -15}$} {=k\ とおくと,\ 図形的には定点を通る直線で,\ kは直線の傾きを意味する.} 分数の形がわかりにくければ,\ y-1=k(x+1)\ と考えてもよい. {定点(-1,\ 1)を通るよう直線の傾きを変化させ,\ kがとりうる値の範囲を求める.}

