
最後の問題では平均点を数学力の指標とするものと解釈してください。
仮説検定の考え方は$数I}:データの分析$で学習済みなので,\ 必要ならば復習してきてほしい.
数Bでは,\ 正規分布を利用する仮説検定を取り扱う. \\
仮説検定 得られたデータを元に仮説を立て,\ それの妥当性を判定する統計的手法
有意水準 ある出来事が起こる確率が偶然とは考えにくいと判断する基準となる確率
普通0.05\,(5\%)とし,\ 慎重を期したい場合には0.01\,(1\%)とすることが多い. \\
正規分布を利用する仮説検定の手順 (仮説:h}ypothesis)
[1]\ \ 統計的に正しいか否かを判断したい仮説H$_1}$\,(対立仮説)を立てる.
[2]\ \ 仮説H$_1}$を否定する仮説H$_0}$\,(帰無仮説)を立てる.
[3]\ \ 有意水準をあらかじめ定め,\ 仮説H$_0}$が棄却される範囲}($棄却域$)を求める.
[4]\ \ 仮説H$_0}$の元で,\ 標本平均$ X$の値を標準化した確率変数$Z}$の値に変換する.
[5]\ \ $\left[ll}
Zが棄却域に入る & →\ \ 仮説H}_0を棄却し,\ 仮説H}_1が妥当と判断する.
Zが棄却域に入らない & →\ \ 仮説H}_0は棄却されない(結論を保留).
両側検定と片側検定
両側検定 棄却域を分布の両側に設定する検定
片側検定 棄却域を分布の片側に設定する検定 \\
出題が常に有意水準5\%や1\%とは限らないので,\ 棄却域を自分で導けるようにしておく必要がある.
以下に,\ 有意水準5\%の場合の棄却域の求め方を示す.\ \ 1\%の場合も同様である.
標準正規分布N(0,\ 1)において,\ 確率5\%でしか起こりえない確率変数Zの範囲が棄却域である.
逆に,\ 確率95\%で起こりえる確率変数Zの範囲を求めることにする.
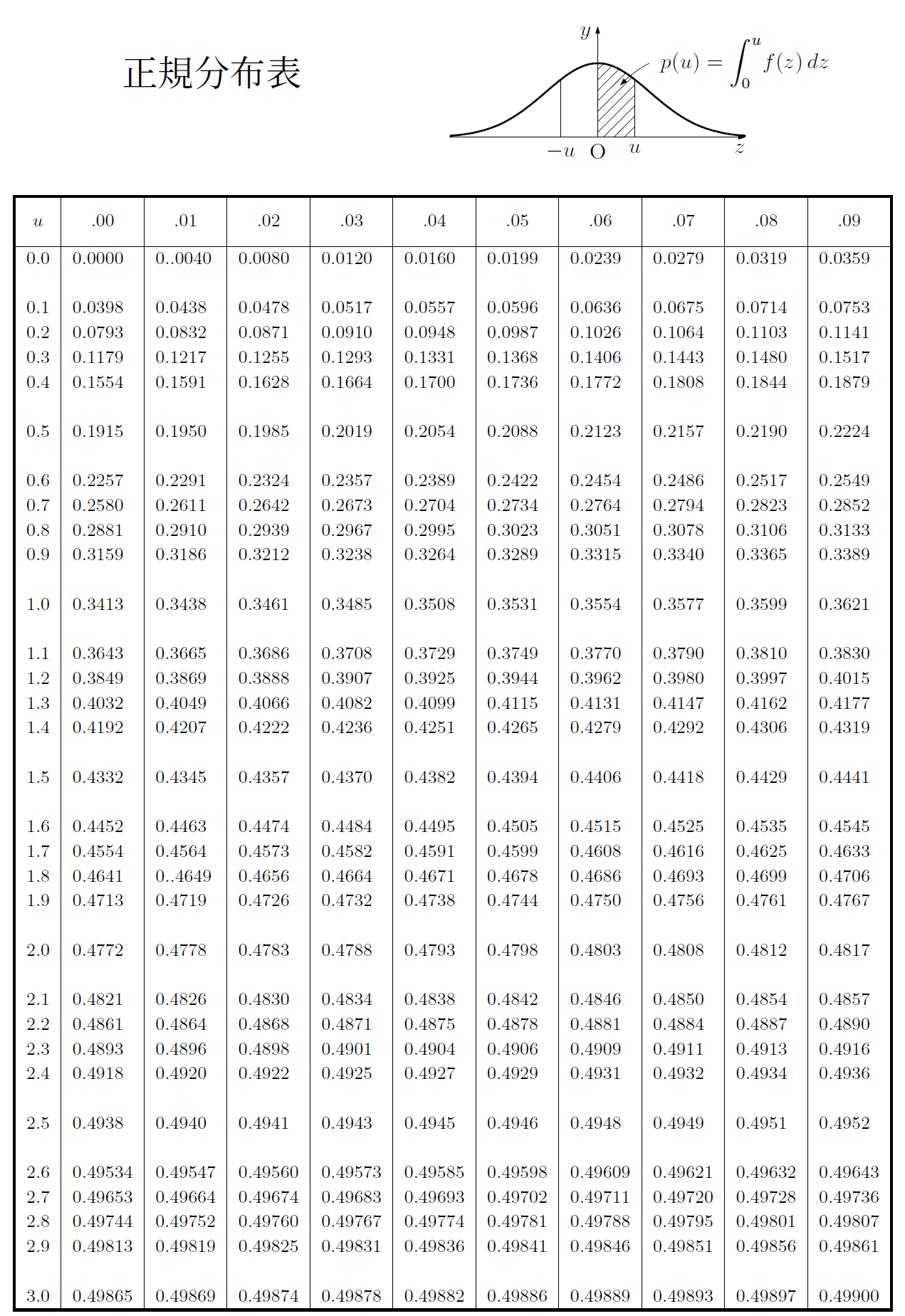
両側検定の場合 P(-\,u≦ Z≦ u)≒0.95
よって,\ P(0≦ Z≦ u)≒0.95÷2=0.475であり,\ 正規分布表よりu=1.96である.
つまり,\ P(-\,1.96≦ Z≦ 1.96)≒0.95より,\ 棄却域はZ≦-\,1.96,\ 1.96≦ Z}となる.
片側検定の場合 P(Z≦ u)=P(Z≦0)+P(0≦ Z≦ u)=0.5+P(0≦ Z≦ u)≒0.95
よって,\ P(0≦ Z≦ u)≒0.95-0.5=0.45であり,\ 正規分布表よりu=1.64である.
つまり,\ P(Z≦1.64)≒0.95より,\ 棄却域はZ≧1.64}となる.
ある会社で製造されている缶詰には内容量200gとの表記がある. この缶詰を100個を
購入して測定したところ,\ 標本平均は199g,\ 標本標準偏差は5gであった.\ 缶詰の表記
が誤りであるといえるかを有意水準5\%と有意水準1\%で検定せよ. \\
{対立仮説H$_1$を「表記は誤りである(母平均$m≠200$g)」}とする.
帰無仮説H$_0$を「表記は誤りではない(母平均$m=200$g)」}とする.
100個は十分に大きい.
よって,\ 仮説H$_0$の元で,\ 標本平均$ X$は近似的に正規分布$N-.2zw}200,\ 5^2}{100}$に従う.
ゆえに,\ $Z= X-200}{5}{10$は近似的に標準正規分布$N(0,\ 1)$に従う.
$P(-\,1.96≦ Z≦1.96)≒0.95$より,\ 有意水準5\%の棄却域は\ \ $Z≦-\,1.96,\ 1.96≦ Z}$
$ X=199$のとき$Z}=199-200}{5}{10=-\,2}$であるから,\ 帰無仮説H$_0$は棄却される.}
つまり,\ 内容量200gとの表記が誤りであると判断してよい.}
$P(-\,2.58≦ Z≦2.58)≒0.99$より,\ 有意水準1\%の棄却域は\ \ $Z≦-\,2.58,\ 2.58≦ Z}$
$ X=199$のとき$Z}=199-200}{5}{10=-\,2}$であるから,\ 帰無仮説H$_0$は棄却されない.}
つまり,\ 内容量200gとの表記が誤りであるとは判断できない.} \\
対立仮説H_1}\,は,\ 基本的には「bf Aとbf Bに差がある(A≠ B})」}という内容の主張になる.
すると,\ 帰無仮説H_0}\,が「A=B}」}という明白な内容の主張になり,\ 議論の出発点にできる.
母平均をm,\ 母標準偏差を\,σ,\ 標本の大きさをnとする.
nが大きいとき,\ 標本平均\, X\,は近似的に正規分布N-.2zw}m,\ σ^2}{n}に従うのであった(中心極限定理).
よって,\ Z= X-m}{σ}{√ n\,は近似的に標準正規分布N(0,\ 1)に従う. [-.8zh]
母平均の区間推定と同様,\ nが大きいとき,\ 母標準偏差\,σ\,を標本標準偏差Sで代用してよい.}
両側検定か片側検定かが問題で指定されていない場合,\ 問題文を元に自分で判断することになる.
本問のように,\ 「\,mが200か否か」だけに関心がある場合は両側に棄却域をとる(両側検定).
「\,mが200より大きいか(小さくはない前提)」を検証する場合,\ 上側に棄却域をとる(片側検定).
「\,mが200より小さいか(大きくはない前提)」を検証する場合,\ 下側に棄却域をとる(片側検定).
棄却域(1.96という値)を暗記しておき,\ 解答のような記述を素早く行うことが望ましい.
有意水準5\%の場合,\ 標本調査で得られたZの値が棄却域に入る.
確率的に不自然であるため,\ 前提の帰無仮説H_0}\,は棄却され,\ 対立仮説H_1}\,が採択される.
有意水準1\%の場合,\ Zの値が棄却域に入らず,\ 前提の帰無仮説H_0}\,は棄却されない.
このとき,\ 棄却されないことが帰無仮説が正しいことをも意味するわけではない}ことに注意する.
棄却と判断するに足る十分な証拠が得られなかっただけで,\ 正しいことにはならないのである.
結局,\ 「対立仮説と帰無仮説のどちらが正しいかはわからない」が最終結論}となる.
有意水準が何\%かや両側か片側かで棄却域が異なり,\ 同じZでも棄却されたりされなかったりする.
有意水準や検定方式は前もって決めておくべき}ものである.
検定後に自分の希望する結論になるように作為的に変更することは許されない.
参考までに,\ 仮説検定の際に犯す可能性がある2種類の判断の誤り}をまとめると以下となる.
& 帰無仮説が正しい & \ 帰無仮説は誤り\
帰無仮説を棄却する & 第一種の過誤} & 正しい判断
帰無仮説を棄却しない & 正しい判断 & 第二種の過誤} \\
本問では,\ 有意水準5\%の場合,\ Z=-\,2は確率的に不自然として帰無仮説H_0}\,を棄却した.
しかし,\ 5\%以下の確率でしか起こりえない偶然が今回起こってしまった可能性もないとはいえない.
この場合,\ 実際には帰無仮説が正しいにもかかわらず,\ 棄却してしまったことになる(第一種の過誤).
有意水準5\%では,\ 5\%以下の確率の偶然が実際に起こってしまうとこの誤りを犯す危険がある.
このため,\ 有意水準のことを危険率}ともいう.
第一種の過誤を犯したくないならば,\ 有意水準より小さく,\ 例えば1\%に設定して検定すればよい.
このとき,\ 第一種の過誤の危険性は減る一方で,\ 「結論を保留」という結果になる可能性が高くなる.
すると,\,実際には帰無仮説が誤りであるのに棄却されない(第二種の過誤)が起こる可能性も高くなる.
このように,\ 2つの過誤はトレードオフの関係にあり,\ 両方の確率を小さくすることはできない.
100個は十分に大きい.
よって,\ 仮説H$_0$の元で,\ 標本平均$ X$は近似的に正規分布$N-.2zw}200,\ 5^2}{100}$に従う.
有意水準5\%の棄却域は \\
$ X=199$であるから,\ 帰無仮説H$_0$は棄却される.} \\100個は十分に大きい.
よって,\ 仮説H$_0$の元で,\ 標本平均$ X$は近似的に正規分布$N-.2zw}200,\ 5^2}{100}$に従う.
ゆえに,\ $Z= X-200}{5}{10$は近似的に標準正規分布$N(0,\ 1)$に従う. 本質的に同じだが,\ 本解と表現の異なる別解を2つ示した.\ 本解とかぶる一部記述は省略.
問題で強制的に誘導される可能性もあるのでいずれも理解しておく必要がある.
別解1は,\ 棄却域をZではなく直接\, X\,で考える}ものである.
別解2は,\ 仮説H_0}\,の元で問題の標本平均を境界とする確率を求め,\ 有意水準と比較する}ものである.
実際には,\ X=199のように\, X\,が母平均m=200と1\,\dot{以}\dot{上}離れることがどれほど稀なのかを考える.
つまり,\ 標本平均\, X\,が母平均m=200と1\,\dot{以}\dot{上}離れる確率P(\, X-200}≧1)を求めることになる.
これが有意水準0.05よりも小さいなら\, X=199は確率的に不自然で,\ 前提の仮説H_0}\,は棄却される.
全国で行われたある試験の平均点は60点,\ 標準偏差は20点であった.\ \ A市の受験生の
中から無作為に選んだ100人の数学の平均点は64点であった.\ \ A市の受験生の数学力
は全国水準を上回っているといえるかを有意水準5\%で検定せよ. \\
対立仮説H$_1$を「A市の平均点$m$は全国平均60点より高い$(m>60)$」}とする.
帰無仮説H$_0$を「A市の平均点$m$は全国平均と同じ60点である$(m=60)$」}とする.
100人は十分に大きい.
よって,\ 仮説H$_0$の元で標本平均$ X$は近似的に正規分布$N-.2zw}60,\ 20^2}{100}$に従う.
ゆえに,\ $Z= X-60}{20}{10$は標準正規分布$N(0,\ 1)$に従う.
$P(Z≦1.64)≒0.95$より,\ 有意水準5\%の棄却域は $Z≧1.64}$
$ X=64$のとき$Z}=64-60}{20}{10=2}$であるから,\ 帰無仮説H$_0$は棄却される.}
つまり,\ A市の受験生の数学力は全国水準を上回っていると判断してよい.
60点か否かではなく,\ 下回っていることはない前提で60点を上回っているかの検証と考えられる.
よって,\ 上側に棄却域をとる片側検定が適切である.

