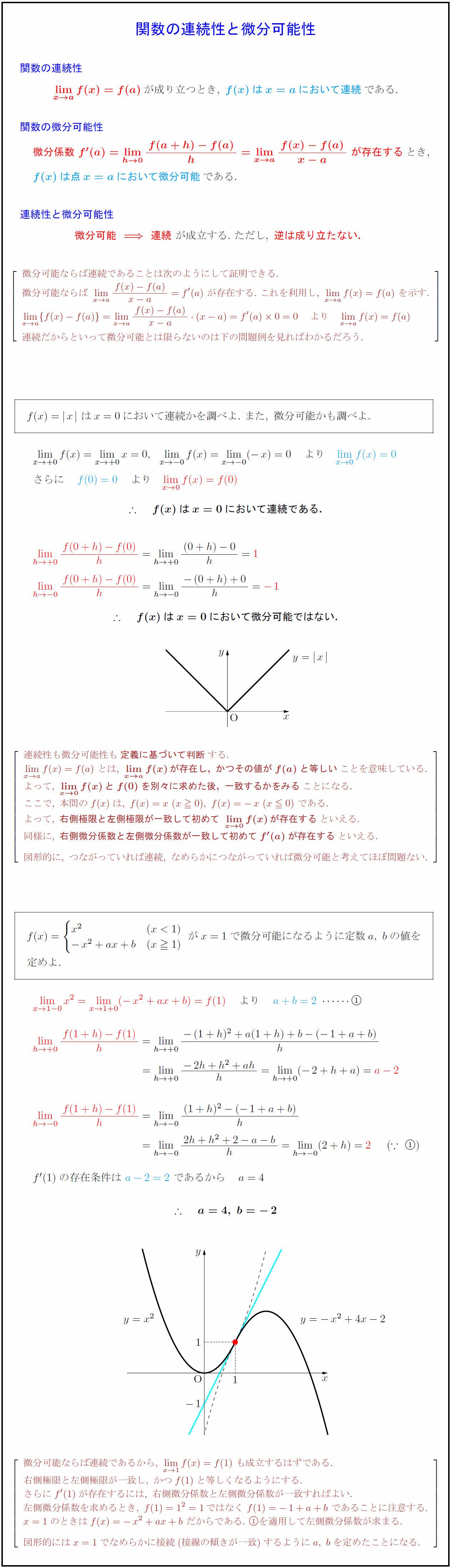
f(x)はx=aにおいて連続である.$} ${微分係数\ f'(a)=lim[h→0]{f(a+h)-f(a)}{h}=limx→ a}{f(x)-f(a)}{x-a}\ が存在するとき,$ ${f(x)は点x=aにおいて微分可能である. ${微分可能連続\ が成立する.\ ただし,\ {逆は成り立たない.$ 微分可能ならば連続であることは次のようにして証明できる. 微分可能ならば\ limx→ a}{f(x)-f(a)}{x-a}=f'(a)\ が存在する. 連続だからといって微分可能とは限らないのは下の問題例を見ればわかるだろう. $f(x)=x}\ はx=0において連続かを調べよ.\ また,\ 微分可能かも調べよ.$ $ {f(x)はx=0において連続である.}$} 連続性も微分可能性も{定義に基づいて判断}する. limx→ a}f(x)=f(a)\ とは,\ {limx→ a}f(x)が存在し,\ かつその値がf(a)と等しい}ことを意味している. よって,\ {lim[x→0]f(x)とf(0)を別々に求めた後,\ 一致するかをみる}ことになる. ここで,\ 本問のf(x)は,\ f(x)=x\ (x0),\ f(x)=-x\ (x0)\ である. よって,\ {右側極限と左側極限が一致して初めて\ lim[x→0]f(x)が存在する}といえる. 同様に,\ {右側微分係数と左側微分係数が一致して初めてf'(a)が存在する}といえる. 図形的に,\ つながっていれば連続,\ なめらかにつながっていれば微分可能と考えてほぼ問題ない. がx=1で微分可能になるように定数a,\ bの値を$ 微分可能ならば連続であるから,\ limx→1}f(x)=f\ も成立するはずである. 右側極限と左側極限が一致し,\ かつfと等しくなるようにする. さらにf’が存在するには,\ 右側微分係数と左側微分係数が一致すればよい. 左側微分係数を求めるとき,\ f=1²=1ではなく\ f=-1+a+b\ であることに注意する. x=1のときはf(x)=-x²+ax+b\ だからである.\ を適用して左側微分係数が求まる. 図形的にはx=1でなめらかに接続(接線の傾きが一致)するようにa,\ bを定めたことになる.

