本解の考え方は高難度なので上級者以外はスルーしてください。別解は簡単です。
中央付近で f(π/2)<f(-α) とありますが、 f(-π/2)<f(-α) の誤りですm(_ _)m
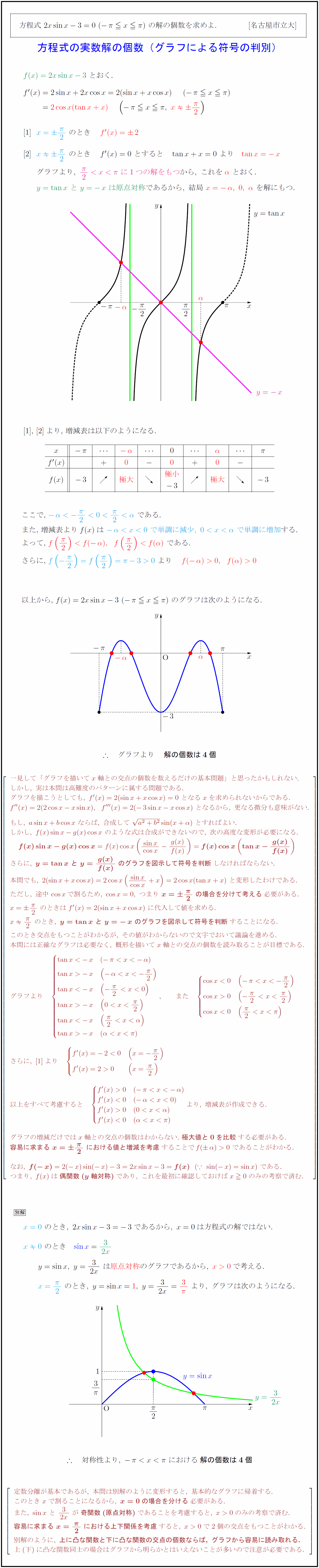
また,\ 増減表より$f(x)は で単調に減少,\で単調に増加}する.$
よって である.$
{解の個数は4個}$}
$[l}
一見して「グラフを描いてx軸との交点の個数を数えるだけの基本問題」と思ったかもしれない.
しかし,\ 実は本問は高難度のパターンに属する問題である.
グラフを描こうとしても,\ f'(x)=2(sin x+xcos x)=0\ となるxを求められないからである.
f”(x)=2(2cos x-xsin x),f”'(x)=2(-3sin x-xcos x)\ となるから,\ 更なる微分も意味がない.
もし,\ asin x+bcos x\ ならば,\ 合成して\ {a²+b²}sin(x+α)\ とすればよい.
しかし,\ f(x)sin x-g(x)cos x\ のような式は合成ができないので,\ 次の高度な変形が必要になる.
{f(x)sin x-g(x)cos x}=f(x)cos x({sin x}{cos x}-{g(x)}{f(x)})={f(x)cos x(tan x-{g(x)}{f(x)})}
さらに,\ {y=tan x\ と\ y={g(x)}{f(x)}\ のグラフを図示して符号を判断}しなければならない.
本問でも,\ 2(sin x+xcos x)=2cos x({sin x}{cos x}+x)=2cos x(tan x+x)\ と変形したわけである.
ただし,\ 途中cos xで割るため,\ cos x=0,\ つまり\ {x={π}{2}\ の場合を分けて考える}必要がある.
x={π}{2}\ のときはf'(x)=2(sin x+xcos x)\ に代入して値を求める.
x{π}{2}\ のとき,\ {y=tan x\ と\ y=-x\ のグラフを図示して符号を判断}することになる.
このとき交点をもつことがわかるが,\ その値がわからないので文字でおいて議論を進める.
本問には正確なグラフは必要なく,\ 概形を描いてx軸との交点の個数を読み取ることが目標である.
より,\ 増減表が作成できる.
グラフの増減だけではx軸との交点の個数はわからない.\ {極大値と0を比較}する必要がある.
{容易に求まる\ x={π}{2}\ における値と増減を考慮}することでf(α)>0\ であることがわかる.
なお,\ {f(-x)}=2(-x)sin(-x)-3=2xsin x-3={f(x)}(∵\ sin(-x)=sin x)\ である.
つまり,\ f(x)は{偶関数(y軸対称)}であり,\ これを最初に確認しておけばx0のみの考察で済む.
2xsin x-3=-3であるから,\ x=0は方程式の解ではない.$
$y=sin x,\ y={3}{2x}\ は原点対称}のグラフであるから,\ x>0}で考える.
$ 対称性より,\ -π0のみの考察で済む.
{容易に求まる\ x={π}{2}\ における上下関係を考慮}すると,\ x>0で2個の交点をもつことがわかる.
別解のように,\ {上に凸な関数と下に凸な関数の交点の個数ならば,\ グラフから容易に読み取れる.}
上(下)に凸な関数同士の場合はグラフから明らかとはいえないことが多いので注意が必要である.

