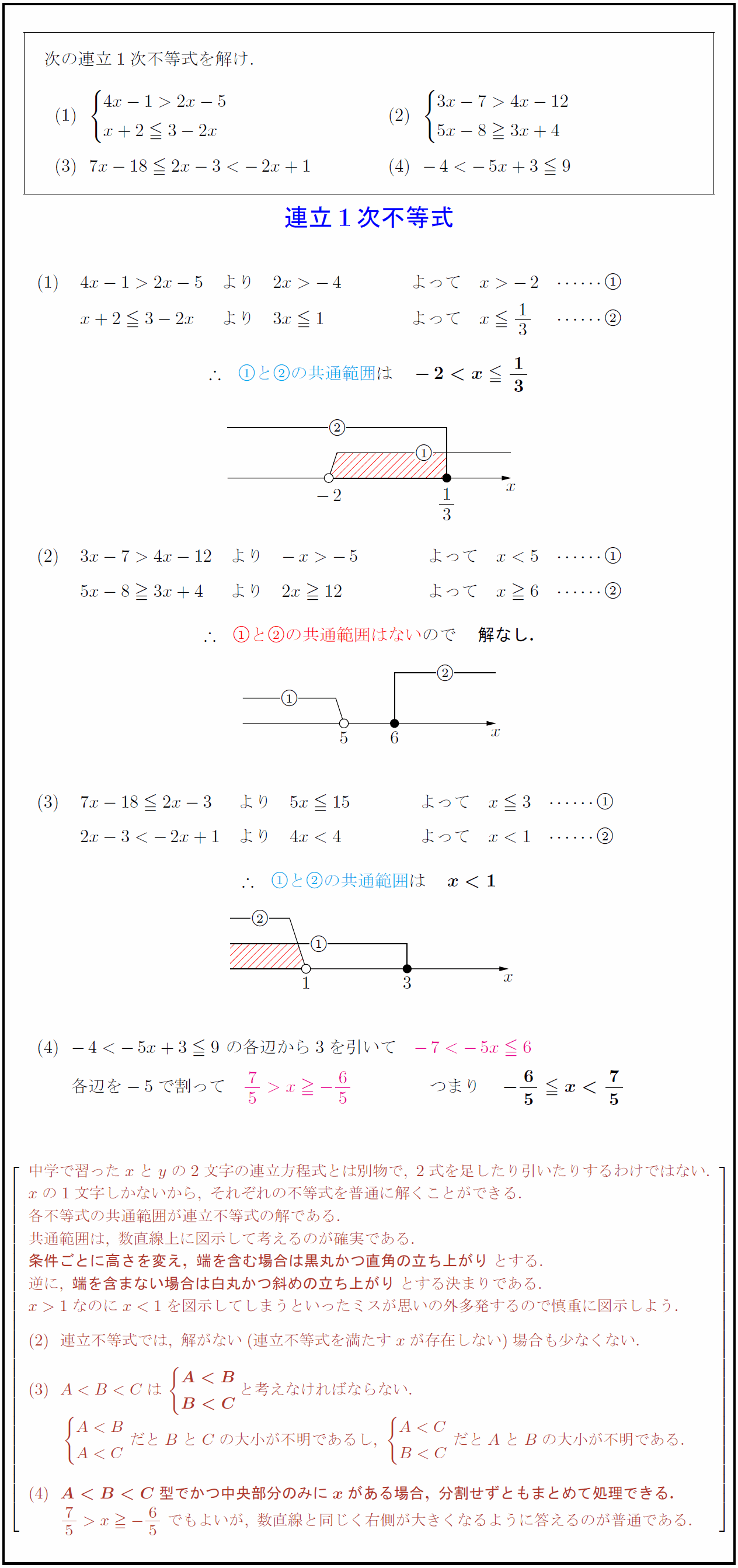
中学で習ったxとyの2文字の連立方程式とは別物で,\ 2式を足したり引いたりするわけではない. xの1文字しかないから,\ それぞれの不等式を普通に解くことができる. 各不等式の共通範囲が連立不等式の解である. 共通範囲は,\ 数直線上に図示して考えるのが確実である. {条件ごとに高さを変え,\ 端を含む場合は黒丸かつ直角の立ち上がり}とする. 逆に,\ {端を含まない場合は白丸かつ斜めの立ち上がり}とする決まりである. x>1なのにx<1を図示してしまうといったミスが思いの外多発するので慎重に図示しよう. は\ {=”” a=”” bx-65\ でもよいが,\ 数直線と同じく右側が大きくなるように答えるのが普通である.

