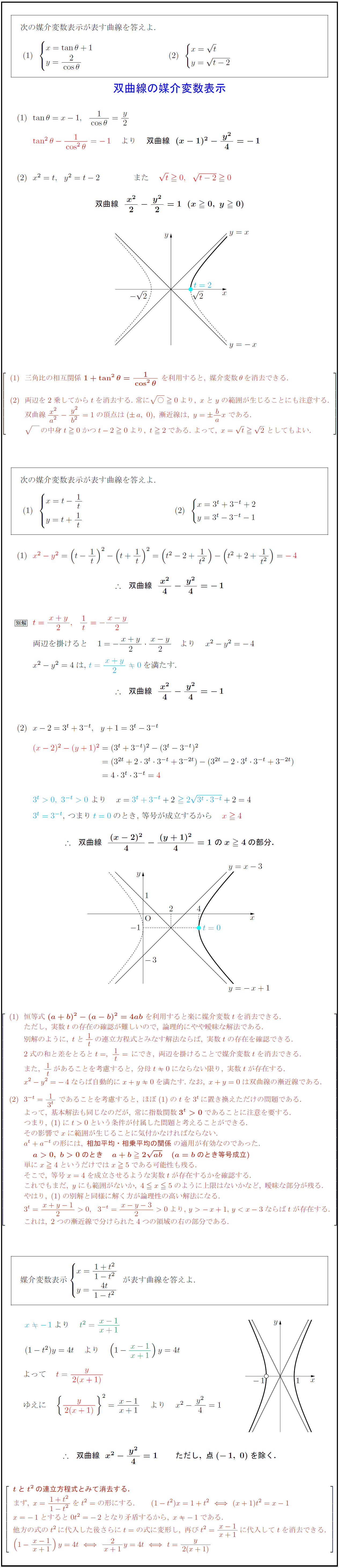
三角比の相互関係\ {1+tan²θ={1}{cos²θ\ を利用すると,\ 媒介変数θを消去できる. 両辺を2乗してからtを消去する.\ 常に{○}0より,\ xとyの範囲が生じることにも注意する. 双曲線{x²}{a²}-{y²}{b²}=1の頂点は(a,\ 0),\ 漸近線は,\ y= bax\ である. の媒介変数表示が表す曲線を答えよ 恒等式\ {(a+b)²-(a-b)²=4ab}\ を利用すると楽に媒介変数tを消去できる. ただし,\ 実数tの存在の確認が難しいので,\ 論理的にやや曖昧な解法である. 別解のように,\ tと1tの連立方程式とみなす解法ならば,\ 実数tの存在を確認できる. 2式の和と差をとるとt=,\ 1t=にでき,\ 両辺を掛けることで媒介変数tを消去できる. また,\ 1tがあることを考慮すると,\ 分母t0にならない限り,\ 実数tが存在する. x²-y²=-4ならば自動的にx+y0を満たす.\ なお,\ x+y=0は双曲線の漸近線である. 3^{-t}={1}{3^t}\ であることを考慮すると,\ ほぼのtを3^tに置き換えただけの問題である. よって,\ 基本解法も同じなのだが,\ 常に指数関数{3^t>0}であることに注意を要する. つまり,\ にt>0という条件が付属した問題と考えることができる. その影響でxに範囲が生じることに気付かなければならない. a^t+a^{-t}の形には,\ {相加平均・相乗平均の関係}の適用が有効なのであった. {a>0,\ b>0のとき a+b2{ab} (a=bのとき等号成立)} 単にx4というだけではx5である可能性も残る. そこで,\ 等号x=4を成立させるような実数tが存在するかを確認する. これでもまだ,\ yにも範囲がないか,\ 4 x5のように上限はないかなど,\ 曖昧な部分が残る. やはり,\ の別解と同様に解く方が論理性の高い解法になる. 3^t={x+y-1}{2}>0,3^{-t}={x-y-3}{2}>0より,y>-x+1,y

