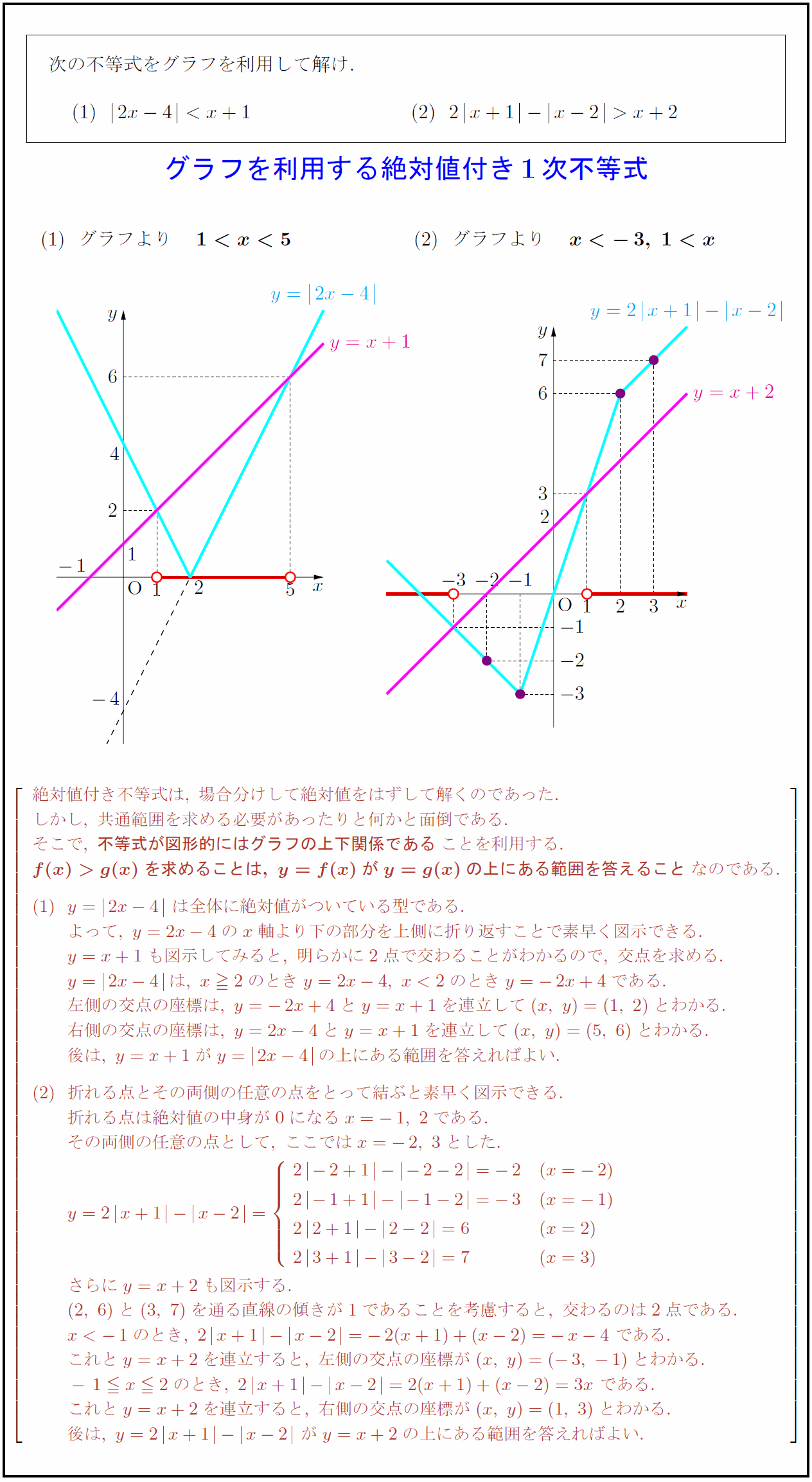
次の不等式をグラフを利用して解け. {グラフを利用する絶対値付き1次不等式 $グラフより {1g(x)を求めることは,\ y=f(x)がy=g(x)の上にある範囲を答えること}なのである. y=2x-4}\ は全体に絶対値がついている型である. よって,\ y=2x-4のx軸より下の部分を上側に折り返すことで素早く図示できる. y=x+1も図示してみると,\ 明らかに2点で交わることがわかるので,\ 交点を求める. y=2x-4}は,\ x2のときy=2x-4,\ x<2のときy=-2x+4である. 左側の交点の座標は,\ y=-2x+4とy=x+1を連立して(x,\ y)=(1,\ 2)とわかる. 右側の交点の座標は,\ y=2x-4とy=x+1を連立して(x,\ y)=(5,\ 6)とわかる. 後は,\ y=x+1がy=2x-4}の上にある範囲を答えればよい. 折れる点とその両側の任意の点をとって結ぶと素早く図示できる. 折れる点は絶対値の中身が0になるx=-1,\ 2である. その両側の任意の点として,\ ここではx=-2,\ 3とした. さらにy=x+2も図示する. (2,\ 6)と(3,\ 7)を通る直線の傾きが1であることを考慮すると,\ 交わるのは2点である. x<-1のとき,\ 2x+1}-x-2}=-2(x+1)+(x-2)=-x-4\ である. これとy=x+2を連立すると,\ 左側の交点の座標が(x,\ y)=(-3,\ -1)とわかる. -1 x2のとき,\ 2x+1}-x-2}=2(x+1)+(x-2)=3x\ である. これとy=x+2を連立すると,\ 右側の交点の座標が(x,\ y)=(1,\ 3)とわかる. 後は,\ y=2x+1}-x-2}\ がy=x+2の上にある範囲を答えればよい.

