以下はGeoGebraによる作図です。スライダーを動かしてみてください。左下のボタンで自動再生もできます。
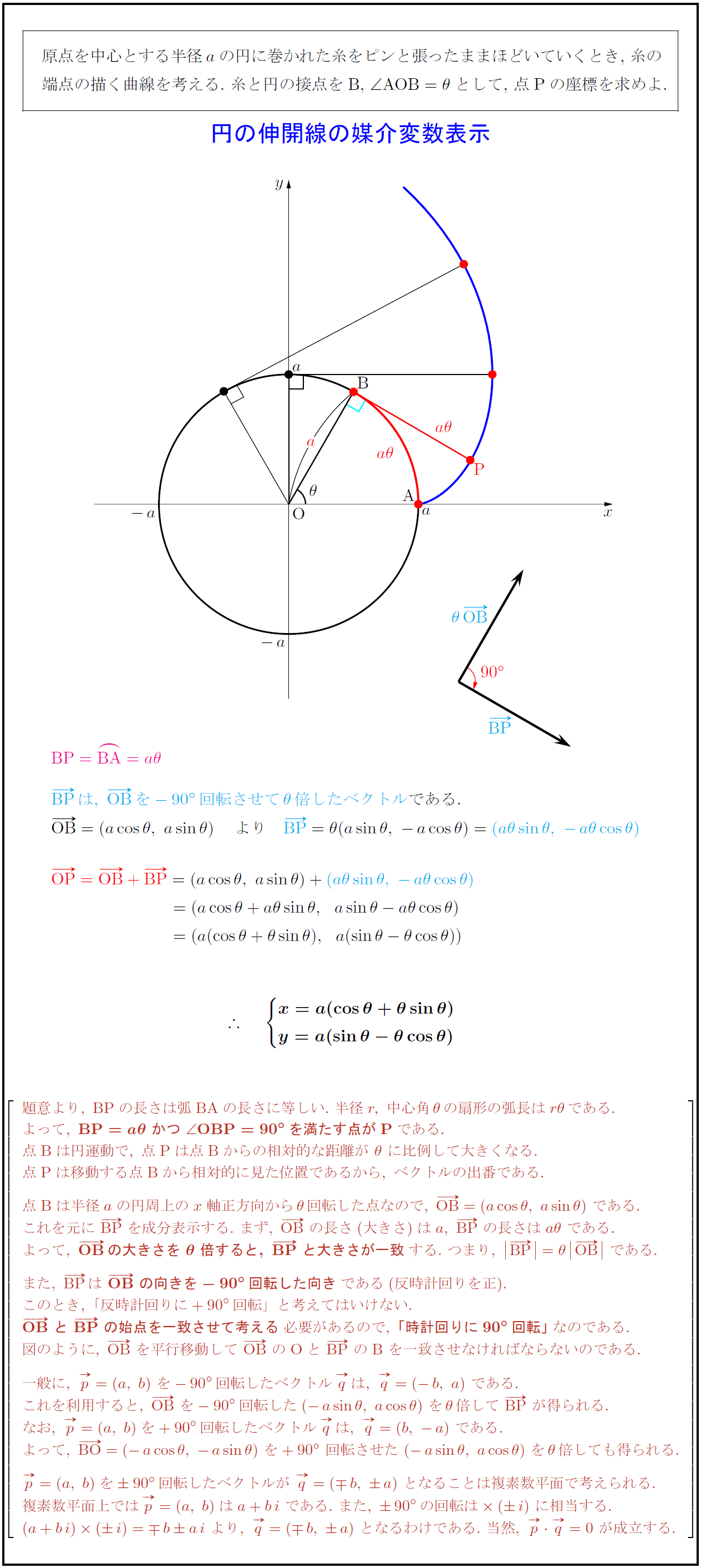
原点を中心とする半径$a$の円に巻かれた糸をピンと張ったままほどいていくとき,\ 糸の 端点の描く曲線を考える.\ 糸と円の接点をB,\ $∠{AOB}=θ$として,\ 点Pの座標を求めよ. 題意より,\ {BP}の長さは弧{BA}の長さに等しい.\ 半径r,\ 中心角θの扇形の弧長はrθである. よって,\ BP}=aθ\ かつ\ ∠{OBP}=90°を満たす点が{Pである. 点{B}は円運動で,\ 点{P}は点{B}からの相対的な距離が\ θ\ に比例して大きくなる. 点{P}は移動する点{B}から相対的に見た位置であるから,\ ベクトルの出番である. 点{B}は半径aの円周上のx軸正方向からθ回転した点なので,\ OB}=(acosθ,\ asinθ)\ である. これを元に\ BP}\ を成分表示する.\ まず,\ OB}\ の長さ(大きさ)はa,\ BP}\ の長さはaθ\ である. よって,\ {OB}の大きさを\ θ\ 倍すると,\ BP}\ と大きさが一致}する.\ つまり,\ BP=θOB\ である. また,\ BP}は\ {OB}\ の向きを-90°回転した向き}である(反時計回りを正). このとき,\ 「反時計回りに+90°回転」と考えてはいけない. {OB}\ と\ BP}\ の始点を一致させて考える}必要があるので,\ {「時計回りに90°回転」}なのである. 図のように,\ OB}\ を平行移動して\ OB}\ の{O}と\ BP}\ の{B}\ を一致させなければならないのである. 一般に,\ p=(a,\ b)\ を-90°回転したベクトルqは,\ q=(-b,\ a)\ である. これを利用すると,\ OB}\ を-90°回転した(-asinθ,\ acosθ)\ をθ倍して\ BP}\ が得られる. なお,\ p=(a,\ b)を+90°回転したベクトルqは,\ q=(b,\ -a)\ である. よって,\ BO}=(-acosθ,\ -asinθ)\ を+90°\ 回転させた\ (-asinθ,\ acosθ)\ をθ倍しても得られる. p=(a,\ b)を90°回転したベクトルが\ q=(±b,\ a)\ となることは複素数平面で考えられる. 複素数平面上ではp=(a,\ b)は{a}+{b}\ である.\ また,\ 90°の回転は (i)\ に相当する. ({a}+{b})(i)={±b}{a}\ より,\ q=(±b,\ a)\ となるわけである.\ 当然,\ pq=0\ が成立する.

