以下はGeoGebraによる作図です。スライダーを動かしてみてください。左下のボタンで自動再生もできます。
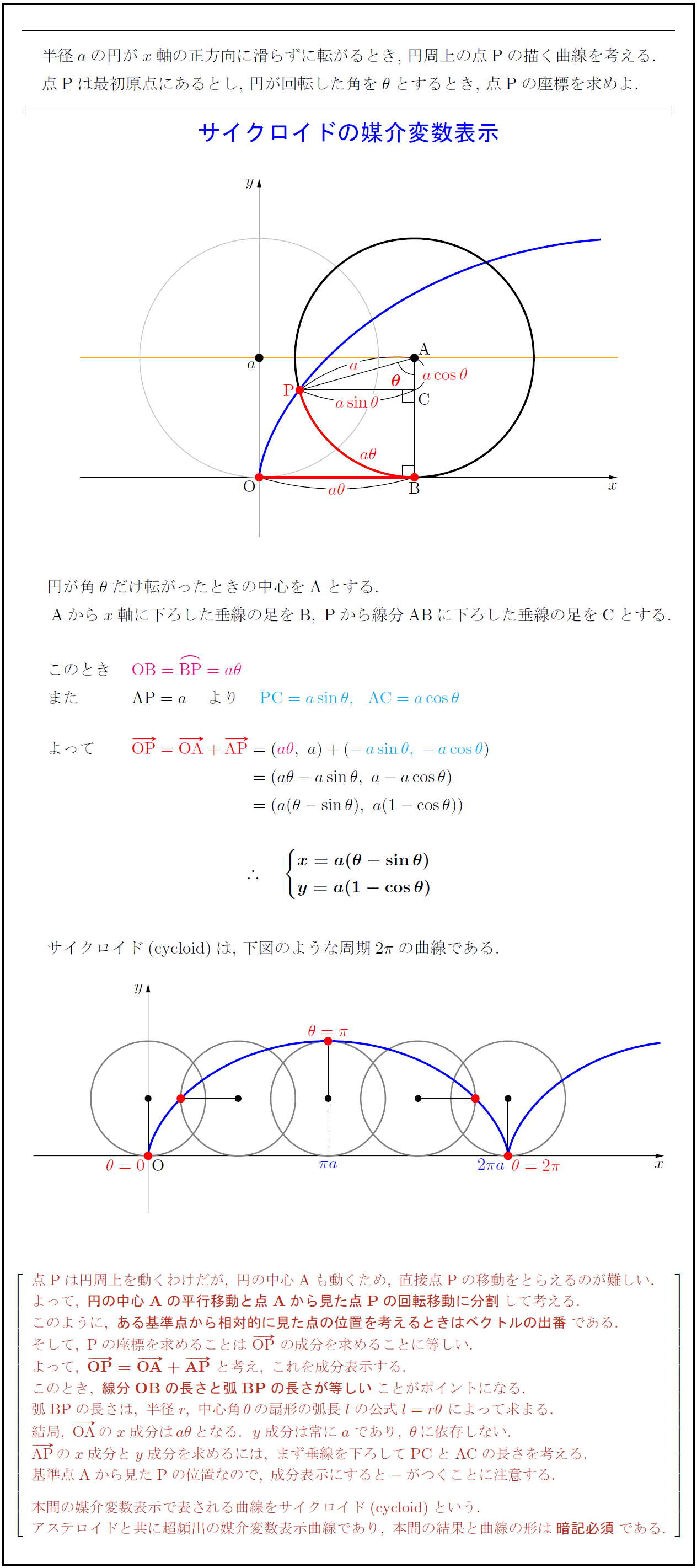
半径$a$の円が$x$軸の正方向に滑らずに転がるとき,\ 円周上の点Pの描く曲線を考える. 点Pは最初原点にあるとし,\ 円が回転した角を$θ$とするとき,\ 点Pの座標を求めよ. 円が角$θ$だけ転がったときの中心をAとする. ${A}からx軸に下ろした垂線の足を{B},\ {P}から線分{AB}に下ろした垂線の足を{C}とする. サイクロイド(cycloid)は,\ 下図のような周期$2π$の曲線である. 点{P}は円周上を動くわけだが,\ 円の中心{A}も動くため,\ 直接点{P}の移動をとらえるのが難しい. よって,\ {円の中心{A}の平行移動と点{A}から見た点{P}の回転移動に分割}して考える. このように,\ {ある基準点から相対的に見た点の位置を考えるときはベクトルの出番}である. そして,\ {P}の座標を求めることは\ OP}\ の成分を求めることに等しい. よって,\ ${OP}=OA}+AP$\ と考え,\ これを成分表示する. このとき,\ {線分{OB}の長さと弧{BP}の長さが等しい}ことがポイントになる. 弧{BP}の長さは,\ 半径r,\ 中心角θの扇形の弧長lの公式l=rθ\ によって求まる. 結局,\ OA}のx成分はaθとなる.y成分は常にaであり,\ θに依存しない. AP}のx成分とy成分を求めるには,\ まず垂線を下ろして{PC}と{AC}の長さを考える. 基準点{A}から見た{P}の位置なので,\ 成分表示にすると-がつくことに注意する. 本問の媒介変数表示で表される曲線をサイクロイド(cycloid)}という. アステロイドと共に超頻出の媒介変数表示曲線であり,\ 本問の結果と曲線の形は{暗記必須}である.

