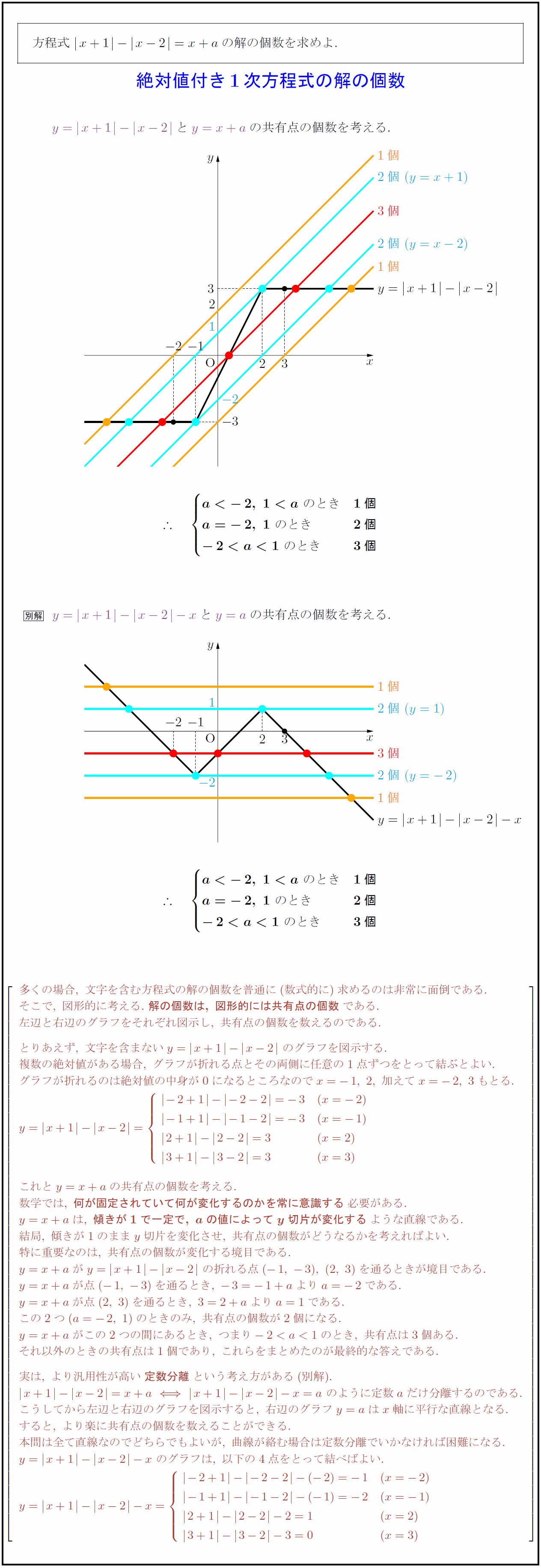
多くの場合,\ 文字を含む方程式の解の個数を普通に(数式的に)求めるのは非常に面倒である. そこで,\ 図形的に考える.\ {解の個数は,\ 図形的には共有点の個数}である. 左辺と右辺のグラフをそれぞれ図示し,\ 共有点の個数を数えるのである. とりあえず,\ 文字を含まないy=x+1}-x-2}\ のグラフを図示する. 複数の絶対値がある場合,\ グラフが折れる点とその両側に任意の1点ずつをとって結ぶとよい. グラフが折れるのは絶対値の中身が0になるところなのでx=-1,\ 2,\ 加えてx=-2,\ 3もとる. これとy=x+aの共有点の個数を考える. 数学では,\ {何が固定されていて何が変化するのかを常に意識する}必要がある. y=x+aは,\ {傾きが1で一定で,\ aの値によってy切片が変化する}ような直線である. 結局,\ 傾きが1のままy切片を変化させ,\ 共有点の個数がどうなるかを考えればよい. 特に重要なのは,\ 共有点の個数が変化する境目である. y=x+aがy=x+1}-x-2}\ の折れる点(-1,\ -3),\ (2,\ 3)を通るときが境目である. y=x+aが点(-1,\ -3)を通るとき,\ -3=-1+aよりa=-2である. y=x+aが点(2,\ 3)を通るとき,\ 3=2+aよりa=1である. この2つ(a=-2,\ 1)のときのみ,\ 共有点の個数が2個になる. y=x+aがこの2つの間にあるとき,\ のとき,\ 共有点は3個ある. それ以外のときの共有点は1個であり,\ これらをまとめたのが最終的な答えである. 実は,\ より汎用性が高い{定数分離}という考え方がある(別解). x+1}-x-2}=x+ax+1}-x-2}-x=a\ のように定数aだけ分離するのである. こうしてから左辺と右辺のグラフを図示すると,\ 右辺のグラフy=aはx軸に平行な直線となる. すると,\ より楽に共有点の個数を数えることができる. 本問は全て直線なのでどちらでもよいが,\ 曲線が絡む場合は定数分離でいかなければ困難になる. y=x+1}-x-2}-x\ のグラフは,\ 以下の4点をとって結べばよい. \

