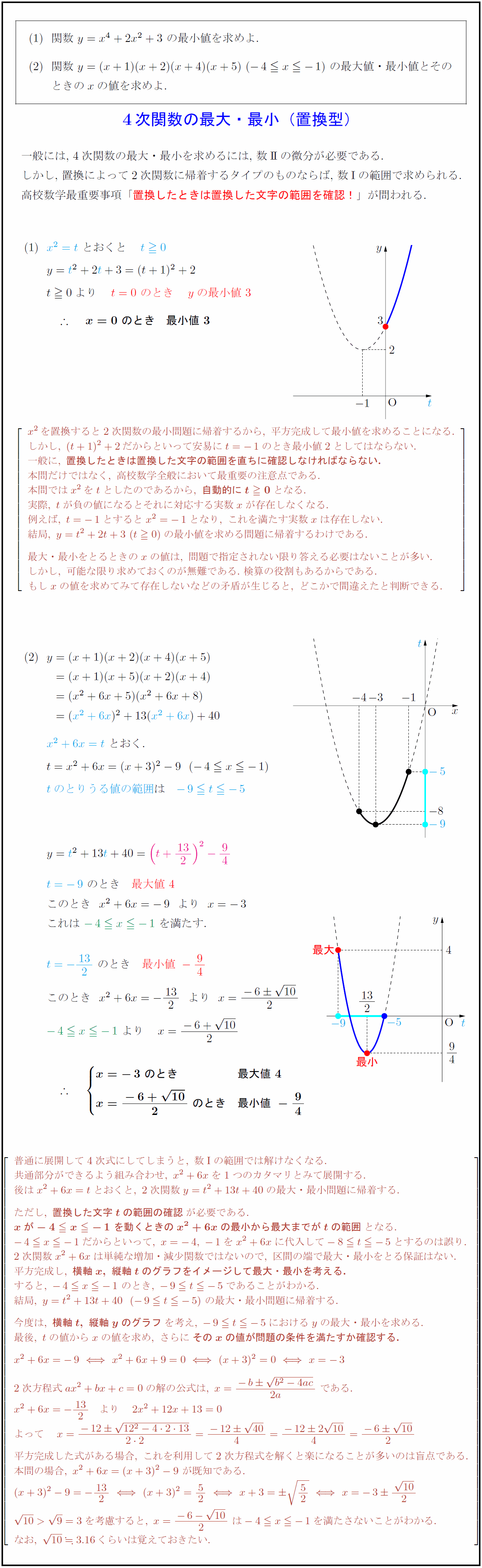
関数\ y=x⁴+2x²+3\ の最小値を求めよ.$ $関数\ y=(x+1)(x+2)(x+4)(x+5)\ (-4 x-1)\ の最大値・最小値とその$ $ときのxの値を求めよ.$ 4次関数の最大・最小(置換型) 一般には,\ 4次関数の最大・最小を求めるには,\ 数IIの微分が必要である. しかし,\ 置換によって2次関数に帰着するタイプのものならば,\ 数Iの範囲で求められる. 高校数学最重要事項「置換したときは置換した文字の範囲を確認!」が問われる. x²を置換すると2次関数の最小問題に帰着するから,\ 平方完成して最小値を求めることになる. しかし,\ (t+1)²+2だからといって安易にt=-1のとき最小値2としてはならない. 一般に,\ {置換したときは置換した文字の範囲を直ちに確認しなければならない.} 本問だけではなく,\ 高校数学全般において最重要の注意点である. 本問ではx²をtとしたのであるから,\ {自動的にt0}となる. 実際,\ tが負の値になるとそれに対応する実数xが存在しなくなる. 例えば,\ t=-1とするとx²=-1となり,\ これを満たす実数xは存在しない. 結局,\ y=t²+2t+3\ (t0)の最小値を求める問題に帰着するわけである. 最大・最小をとるときのxの値は,\ 問題で指定されない限り答える必要はないことが多い. しかし,\ 可能な限り求めておくのが無難である.\ 検算の役割もあるからである. もしxの値を求めてみて存在しないなどの矛盾が生じると,\ どこかで間違えたと判断できる. 普通に展開して4次式にしてしまうと,\ 数 Iの範囲では解けなくなる. 共通部分ができるよう組み合わせ,\ x²+6xを1つのカタマリとみて展開する. 後はx²+6x=tとおくと,\ 2次関数y=t²+13t+40の最大・最小問題に帰着する. ただし,\ {置換した文字tの範囲の確認}が必要である. {xが-4 x-1\ を動くときのx²+6xの最小から最大までがtの範囲}となる. -4 x-1だからといって,\ x=-4,\ -1をx²+6xに代入して-8 t -5とするのは誤り. 2次関数x²+6xは単純な増加・減少関数ではないので,\ 区間の端で最大・最小をとる保証はない. 平方完成し,\ {横軸x,\ 縦軸tのグラフをイメージして最大・最小を考える.} すると,\ -4 x-1\ のとき,\ -9 t-5であることがわかる. 結局,\ y=t²+13t+40(-9 t-5)\ の最大・最小問題に帰着する. 今度は,\ {横軸t,\ 縦軸yのグラフ}を考え,\ -9 t-5におけるyの最大・最小を求める. 最後,\ tの値からxの値を求め,\ さらに{そのxの値が問題の条件を満たすか確認する.} \ 平方完成した式がある場合,\ これを利用して2次方程式を解くと楽になることが多いのは盲点である. 本問の場合,\ x²+6x=(x+3)²-9\ が既知である.

