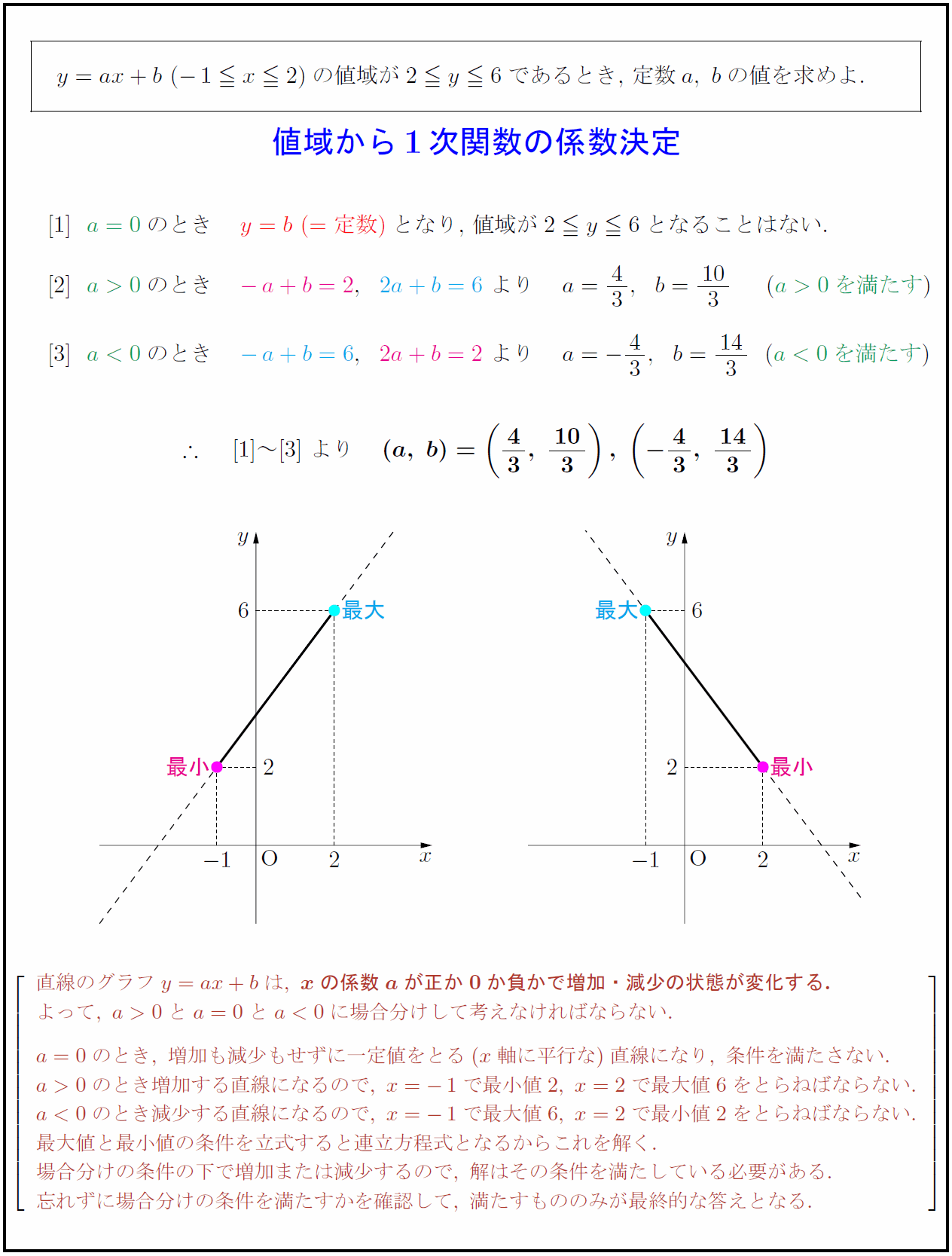
y=ax+b\ (-1 x2)$の値域が$2 y6$であるとき,\ 定数$a,\ b$の値を求めよ. {値域から1次関数の係数決定 $a=0}$のとき $y=b\ (=定数)}$となり,\ 値域が$2 y6$となることはない 直線のグラフy=ax+bは,\ {xの係数aが正か0か負かで増加・減少の状態が変化する.} よって,\ a>0とa=0とa<0に場合分けして考えなければならない. a=0のとき,\ 増加も減少もせずに一定値をとる(x軸に平行な)直線になり,\ 条件を満たさない. a>0のとき増加する直線になるので,\ x=-1で最小値2,\ x=2で最大値6をとらねばならない. a<0のとき減少する直線になるので,\ x=-1で最大値6,\ x=2で最小値2をとらねばならない. 最大値と最小値の条件を立式すると連立方程式となるからこれを解く. 場合分けの条件の下で増加または減少するので,\ 解はその条件を満たしている必要がある. 忘れずに場合分けの条件を満たすかを確認して,\ 満たすもののみが最終的な答えとなる.

