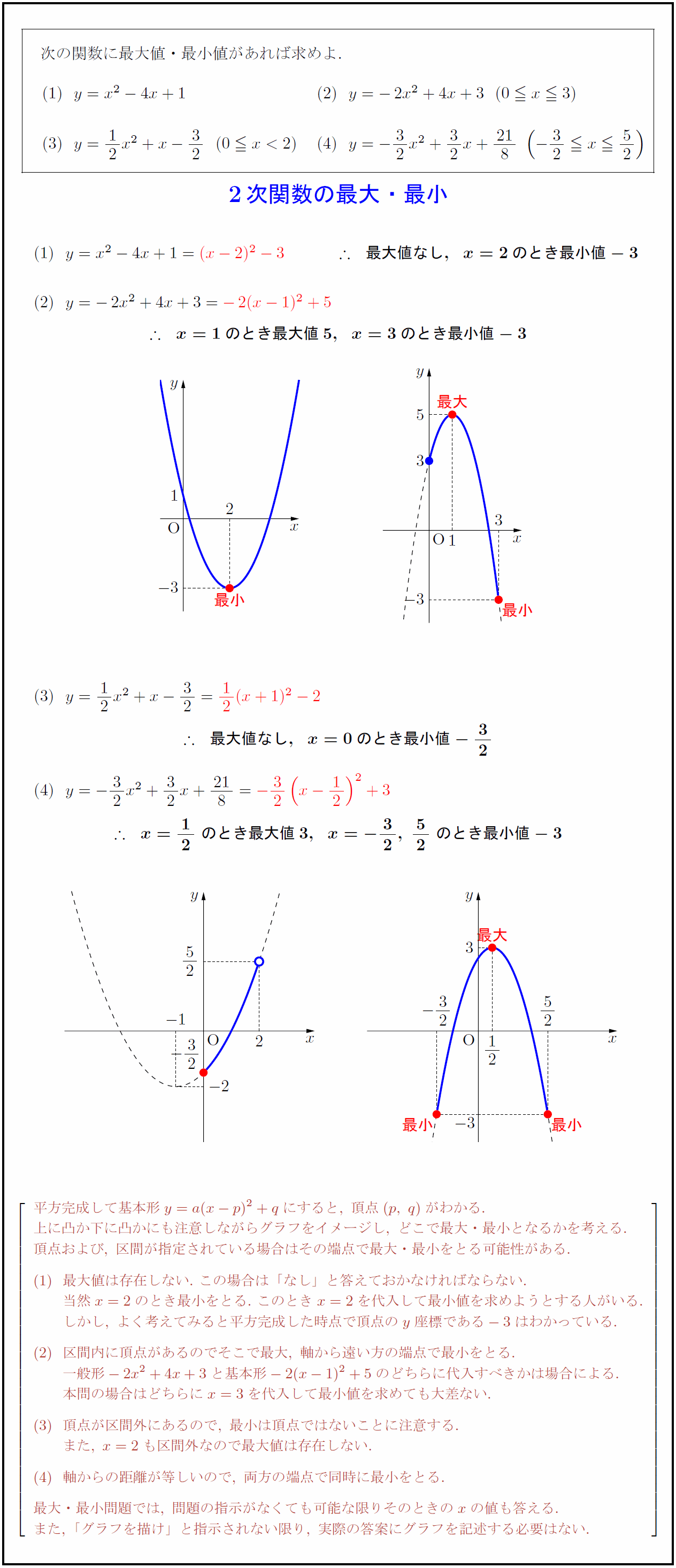
平方完成して基本形y=a(x-p)²+qにすると,\ 頂点(p,\ q)がわかる. 上に凸か下に凸かにも注意しながらグラフをイメージし,\ どこで最大・最小となるかを考える. 頂点および,\ 区間が指定されている場合はその端点で最大・最小をとる可能性がある. 最大値は存在しない.\ この場合は「なし」と答えておかなければならない. 当然x=2のとき最小をとる.\ このときx=2を代入して最小値を求めようとする人がいる. しかし,\ よく考えてみると平方完成した時点で頂点のy座標である-3はわかっている. 区間内に頂点があるのでそこで最大,\ 軸から遠い方の端点で最小をとる. 一般形-2x²+4x+3と基本形-2(x-1)²+5のどちらに代入すべきかは場合による. 本問の場合はどちらにx=3を代入して最小値を求めても大差ない. 頂点が区間外にあるので,\ 最小は頂点ではないことに注意する. また,\ x=2も区間外なので最大値は存在しない. 軸からの距離が等しいので,\ 両方の端点で同時に最小をとる. 最大・最小問題では,\ 問題の指示がなくても可能な限りそのときのxの値も答える. また,\ 「グラフを描け」と指示されない限り,\ 実際の答案にグラフを記述する必要はない.

