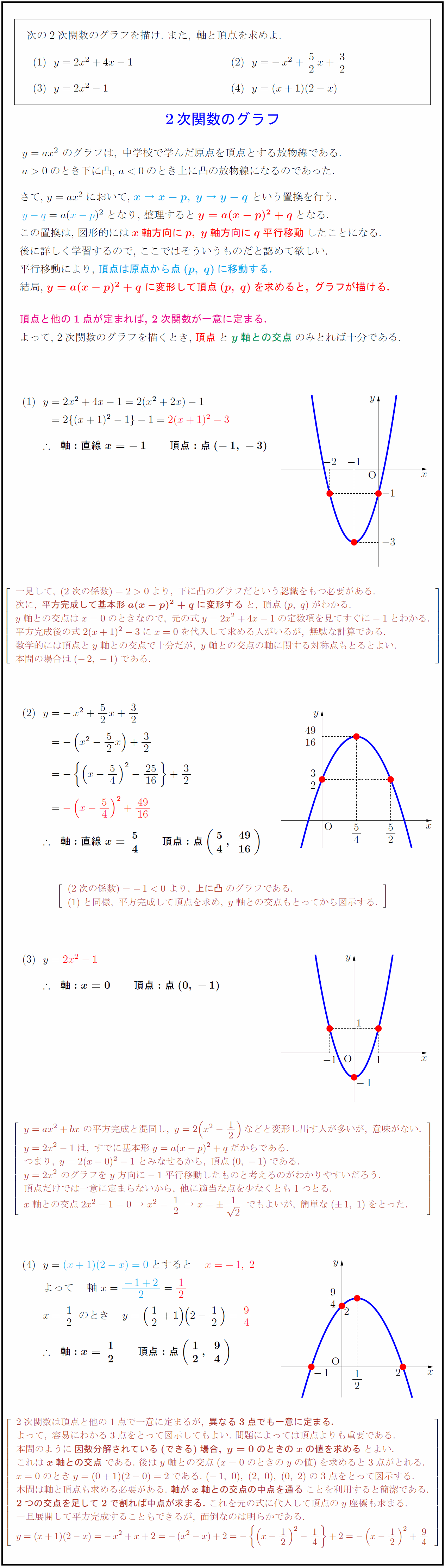
$y=ax²\ のグラフは,\ 中学校で学んだ原点を頂点とする放物線である.$ $a>0$のとき下に凸,\ $a<0$のとき上に凸の放物線になるのであった. さて,\ $y=ax²$において,\ ${x\ →\ x-p,\ y\ →\ y-q$\ という置換を行う. $y-q}=a(x-p})²$となり,\ 整理すると${y=a(x-p)²+q$となる. この置換は,\ 図形的には${x軸方向にp,\ y軸方向にq平行移動$したことになる. 後に詳しく学習するので,\ ここではそういうものだと認めて欲しい. 平行移動により,\ ${頂点は原点から点(p,\ q)に移動する.$ 結局,\ ${y=a(x-p)²+q\ に変形して頂点(p,\ q)を求めると,\ グラフが描ける.$ 頂点と他の1点が定まれば,\ 2次関数が一意に定まる. よって,\ 2次関数のグラフを描くとき,\ ${頂点$と${y軸との交点$のみとれば十分である. $y=2x²+4x-1=2(x²+2x)-1$ { }${y}=2{(x+1)²-1}-1=2(x+1)²-3}$ { }${軸:直線\ x=-1 頂点:点 一見して,\ (2次の係数)=2>0より,\ 下に凸のグラフだという認識をもつ必要がある. 次に,\ {平方完成して基本形a(x-p)²+qに変形する}と,\ 頂点(p,\ q)がわかる. y軸との交点はx=0のときなので,\ 元の式y=2x²+4x-1の定数項を見てすぐに-1とわかる. 平方完成後の式2(x+1)²-3にx=0を代入して求める人がいるが,\ 無駄な計算である. 数学的には頂点とy軸との交点で十分だが,\ y軸との交点の軸に関する対称点もとるとよい. 本問の場合は(-2,\ -1)である. (2次の係数)=-1<0\ より,\ {上に凸}のグラフである. と同様,\ 平方完成して頂点を求め,\ y軸との交点もとってから図示する. y=ax²+bx\ の平方完成と混同し,\ y=2(x²-12)などと変形し出す人が多いが,\ 意味がない. y=2x²-1は,\ すでに基本形y=a(x-p)²+qだからである. つまり,\ y=2(x-0)²-1\ とみなせるから,\ 頂点(0,\ -1)である. y=2x²\ のグラフをy方向に-1平行移動したものと考えるのがわかりやすいだろう. 頂点だけでは一意に定まらないから,\ 他に適当な点を少なくとも1つとる. x軸との交点2x²-1=0\ →\ x²=12\ →\ x={1}{2}\ でもよいが,\ 簡単な(1,\ 1)をとった. 2次関数は頂点と他の1点で一意に定まるが,\ {異なる3点でも一意に定まる.} よって,\ 容易にわかる3点をとって図示してもよい.\ 問題によっては頂点よりも重要である. 本問のように{因数分解されている(できる)場合,\ y=0のときのxの値を求める}とよい. これは{x軸との交点}である.\ 後はy軸との交点(x=0のときのyの値)を求めると3点がとれる. x=0のときy=(0+1)(2-0)=2である.\ (-1,\ 0),\ (2,\ 0),\ (0,\ 2)の3点をとって図示する. 本問は軸と頂点も求める必要がある.\ {軸がx軸との交点の中点を通る}ことを利用すると簡潔である. {2つの交点を足して2で割れば中点が求まる.}\ これを元の式に代入して頂点のy座標も求まる. 一旦展開して平方完成することもできるが,\ 面倒なのは明らかである.

