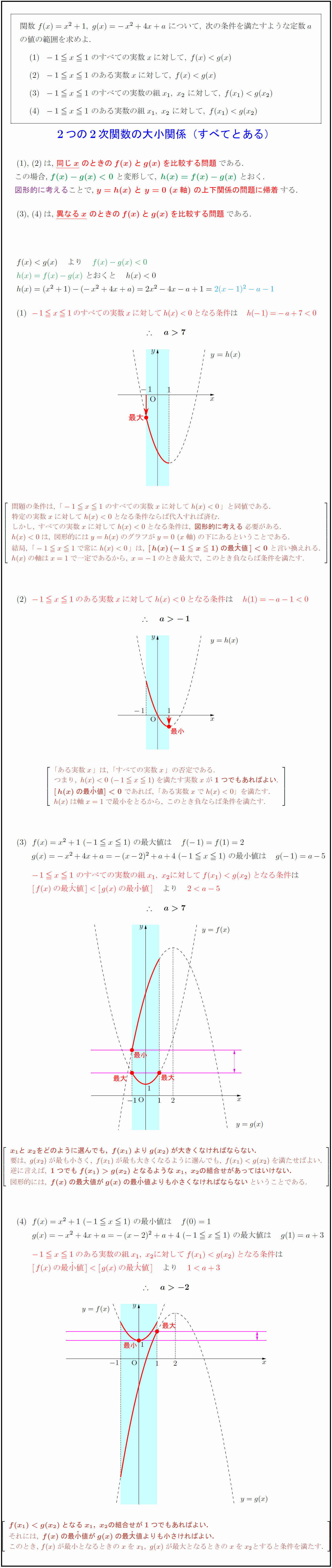
関数\ f(x)=x²+1,\ g(x)=-x²+4x+a\ について,\ 次の条件を満たすような定数a$ $の値の範囲を求めよ.$ $-1 x1\ のすべての実数xに対して,\ f(x)<g(x)$ $-1=”” x1\=”” のある実数xに対して,\=”” f(x)>g(x)$=”” のすべての実数の組x₁,\=”” x₂\=”” に対して,\=”” f(x₁)<g(x₂)$=”” のある実数の組x₁,\=”” \{2つの2次関数の大小関係(すべてとある)=”” ,\=”” は,\=”” $同じ${x}$\=”” {のときのf(x)とg(x)を比較する問題である.$=”” この場合,\=”” ${f(x)-g(x)>0\=”” と変形して,\=”” {h(x)=”f(x)-g(x)\” とおく.$=”” 図形的に考えることで,\=”” ${y=”h(x)\” と\=”” y=”0\” (x軸)\=”” の上下関係の問題に帰着する.$=”” ${異なる${x}$\=”” のときのf(x)とg(x)を比較する問題である.$=”” \=”” 問題の条件は,\=”” 「-1=”” のすべての実数xに対してh(x)<0」と同値である.=”” 特定の実数xに対してh(x)<0となる条件ならば代入すれば済む.=”” すべての実数xに対してh(x)<0となる条件は,\=”” {図形的に考える}必要がある.=”” h(x)<0は,\=”” 図形的にはy=”h(x)のグラフがy=0\” (x軸)の下にあるということである.=”” 結局,\=”” x1で常にh(x)<0」は,\=”” {[h(x)(-1=”” x1)の最大}値]<0}\=”” と言い換えれる.=”” h(x)の軸はx=”1で一定であるから,\” x=”-1のとき最大で,\” このとき負ならば条件を満たす.=”” 「ある実数x」は,\=”” 「すべての実数x」の否定である.=”” つまり,\=”” h(x)<0\=”” を満たす実数xが{1つでもあればよい}.=”” {[h(x)の最小}値]<0}\=”” であれば,\=”” 「ある実数xでh(x)<0」を満たす.=”” h(x)は軸x=”1で最小をとるから,\” {x₁とx₂をどのように選んでも,\=”” f(x₁)よりg(x₂)が大きくなければならない.}=”” 要は,\=”” g(x₂)が最も小さく,\=”” f(x₁)が最も大きくなるように選んでも,\=”” f(x₁)<g(x₂)を満たせばよい.=”” 逆に言えば,\=”” {1つでもf(x₁)>g(x₂)となるようなx₁,\=”” x₂の組合せがあってはいけない.}=”” 図形的には,\=”” {f(x)の最大}値がg(x)の最小}値よりも小さくなければならない}ということである.=”” {f(x₁)<g(x₂)となるx₁,\=”” x₂の組合せが1つでもあればよい.}=”” それには,\=”” {f(x)の最小}値がg(x)の最大}値よりも小さければよい.}=”” このとき,f(x)が最小となるときのxをx₁,\=”” g(x)が最大となるときのxをx₂とすると条件を満たす.

