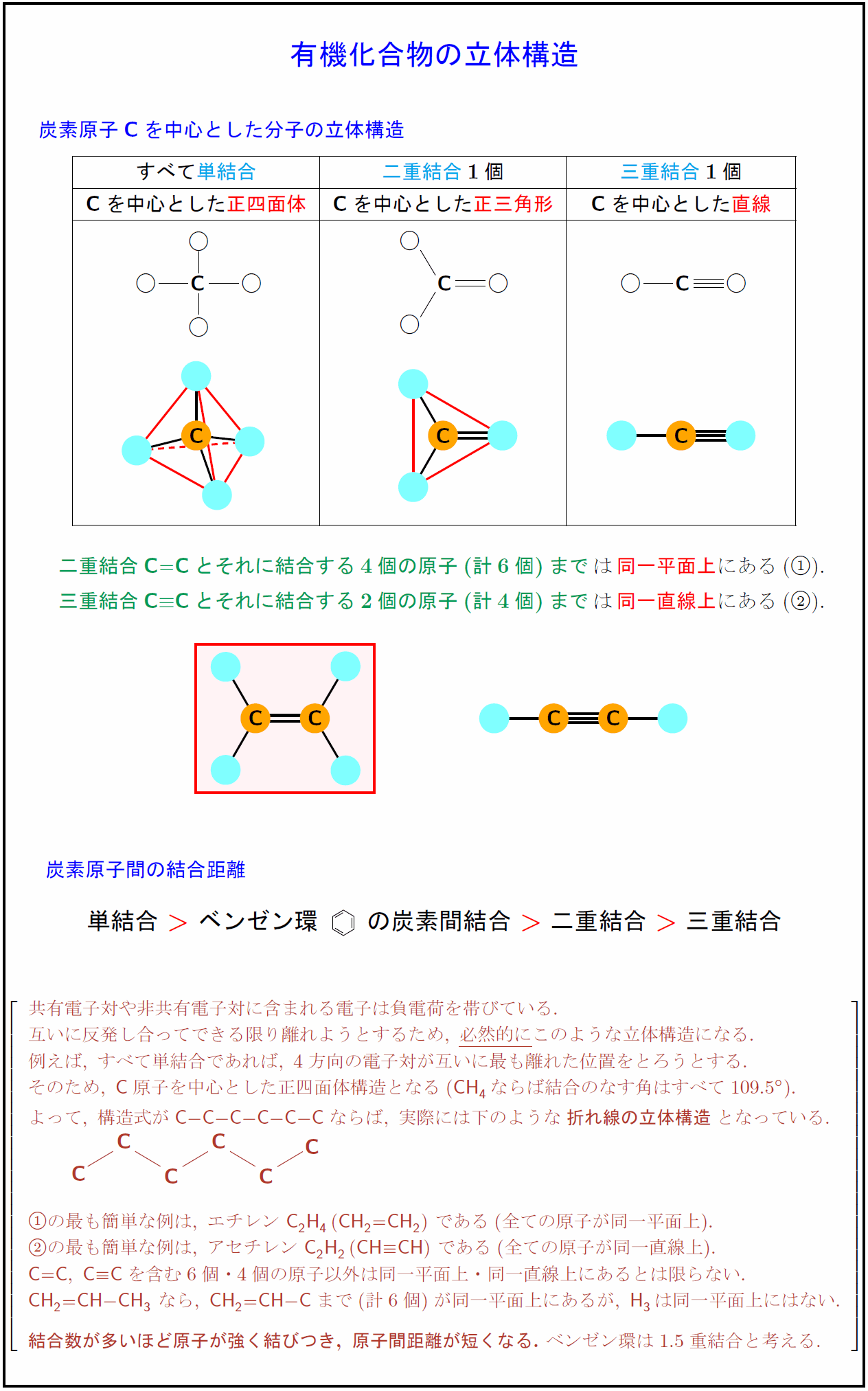
炭素原子{C}を中心とした分子の立体構造 すべて単結合}{二重結合}1個} 三重結合}1個} {C}を中心とした\正四面体}を中心とした正三角形}C}を中心とした直線二重結合{C=C}とそれに結合する4個の原子(計6個)までは同一平面上にある三重結合{C}$≡${C}とそれに結合する2個の原子(計4個)までは{同一直線上にある炭素原子間の結合距離}単結合\ ベンゼン環\parbox[c]{2zw}{\bzdrv{の炭素間結合二重結合三重結合}$ 共有電子対や非共有電子対に含まれる電子は負電荷を帯びている. 互いに反発し合ってできる限り離れようとするため,\ 必然的に}このような立体構造になる. [.2zh] 例えば,\ すべて単結合であれば,\ 4方向の電子対が互いに最も離れた位置をとろうとする. そのため,\ {C}原子を中心とした正四面体構造となる(CH₄ならば結合のなす角はすべて109.5°). よって,\ 構造式が{C-C-C-C-C-C}ならば,\ 実際には下のような{折れ線の立体構造}となっている. \ の最も簡単な例は,\ エチレン\ {C2H4}({CH₂=CH₂})\ である(全ての原子が同一平面上). の最も簡単な例は,\ アセチレン\ {C2H₂}({CH#CH})\ である(全ての原子が同一直線上). {C=C},\ {C#C}を含む6個・4個の原子以外は同一平面上・同一直線上にあるとは限らない. {CH₂=CH-CH₃}\ なら,\ {CH₂=CH-C}まで(計6個)が同一平面上にあるが,\ {H3}は同一平面上にはない. {結合数が多いほど原子が強く結びつき,\ 原子間距離が短くなる.}\ ベンゼン環は1.5重結合と考える.

