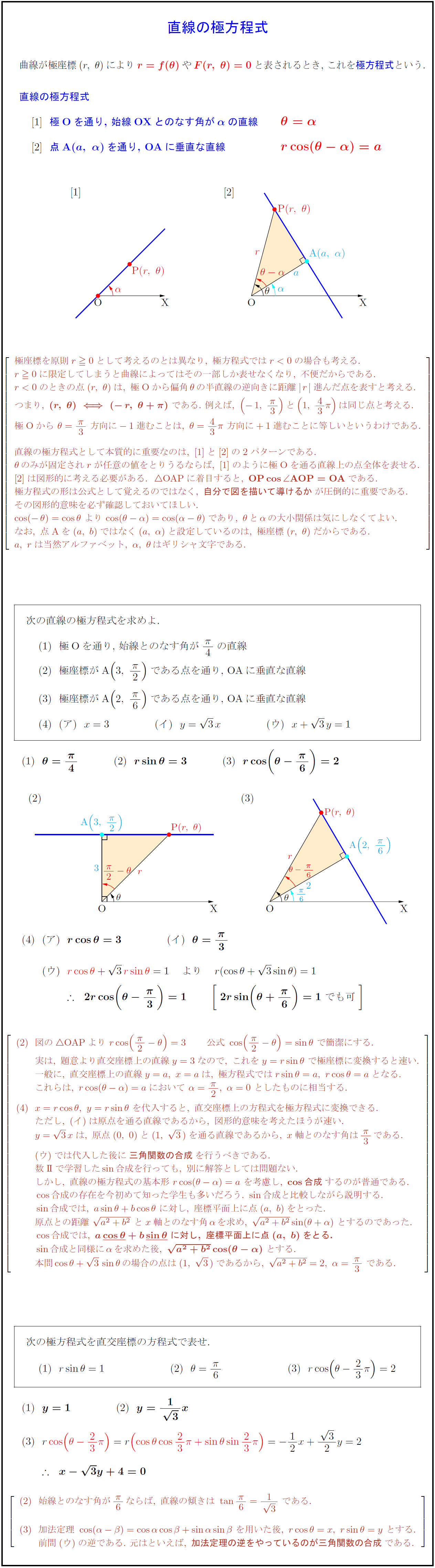
曲線が極座標$(r,{F(r,\ θ)=0$と表されるとき,\ これを極方程式という.}{直線の極方程式極Oを通り,\ 始線OXとのなす角が${α}$の直線点A${(a,\ α)}$を通り,\ OAに垂直な直線 極座標を原則r0として考えるのとは異なり,\ 極方程式ではr<0の場合も考える. r0に限定してしまうと曲線によってはその一部しか表せなくなり,\ 不便だからである. r<0のときの点(r,\ θ)は,\ 極 Oから偏角θの半直線の逆向きに距離 r進んだ点を表すと考える. つまり,\ {(r,\ θ)(-r,\ θ+π)}\ である.\ 例えば,\ (-1,\ {π}{3})と(1,\ 43π)は同じ点と考える. 極 Oから\ θ={π}{3}\ 方向に-1進むことは,\ θ=43π\ 方向に+1進むことに等しいというわけである. 直線の極方程式として本質的に重要なのは,\ との2パターンである. θのみが固定されrが任意の値をとりうるならば,\ のように極 Oを通る直線上の点全体を表せる. は図形的に考える必要がある.{OAPに着目すると,\ {OPcos∠ AOP=OAである. 極方程式の形は公式として覚えるのではなく,\ {自分で図を描いて導けるか}が圧倒的に重要である. その図形的意味を必ず確認しておいてほしい. cos(-θ)=cosθ\ よりcos(θ-α)=cos(α-θ)であり,\ θとαの大小関係は気にしなくてよい. なお,\ 点 Aを(a,\ b)ではなく(a,\ α)と設定しているのは,\ 極座標(r,\ θ)だからである. a,\ rは当然アルファベット,\ α,\ θはギリシャ文字である. }次の直線の極方程式を求めよ. 極Oを通り,\ 始線とのなす角が${π}{4}$の直線 極座標がA$(3,\ {π}{2})$である点を通り,\ OAに垂直な直線 極座標がA$(2,\ {π}{6})$である点を通り,\ OAに垂直な直線 \ 図の{OAP}より\ rcos({π}{2}-θ)=3 公式\ cos({π}{2}-θ)=sinθ\ で簡潔にする. 実は,\ 題意より直交座標上の直線y=3なので,\ これをy=rsinθ\ で極座標に変換すると速い. 一般に,\ 直交座標上の直線y=a,\ x=aは,\ 極方程式ではrsinθ=a,\ rcosθ=aとなる. これらは,\ rcos(θ-α)=aにおいて\ α={π}{2},\ α=0\ としたものに相当する. x=rcosθ,\ y=rsinθ\ を代入すると,\ 直交座標上の方程式を極方程式に変換できる. ただし,\ (イ)は原点を通る直線であるから,\ 図形的意味を考えたほうが速い. y=3xは,\ 原点(0,\ 0)と(1,\ 3)を通る直線であるから,\ x軸とのなす角は{π}{3}である. (ウ)では代入した後に{三角関数の合成}を行うべきである. 数II}で学習した sin 合成を行っても,\ 別に解答としては問題ない. しかし,\ 直線の極方程式の基本形\ rcos(θ-α)=a\ を考慮し,\ {cos 合成}するのが普通である. cos 合成の存在を今初めて知った学生も多いだろう.\ sin 合成と比較しながら説明する. sin 合成では,\ asinθ+bcosθ\ に対し,\ 座標平面上に点(a,\ b)をとった. 原点との距離\ {a²+b²}\ とx軸とのなす角αを求め,\ {a²+b²}sin(θ+α)\ とするのであった. cos 合成では,\ {acosθ}+bsinθ}\ に対し,\ 座標平面上に点(a,\ b)をとる.} sin 合成と同様にαを求めた後,\ a²+b²}cos(θ-α)}\ とする. 本問 cosθ+3sinθの場合の点は(1,\ 3)であるから,\ {a²+b²}=2,\ α={π}{3}\ である. }次の極方程式を直交座標の方程式で表せ. 始線とのなす角が{π}{6}ならば,\ 直線の傾きは\ tan{π}{6}={1}{3}\ である. 加法定理\ cos(α-β)=cosαcosβ+sinαsinβ\ を用いた後,\ rcosθ=x,\ rsinθ=y\ とする. 前問(ウ)の逆である.\ 元はといえば,\ {加法定理の逆をやっているのが三角関数の合成}である.

