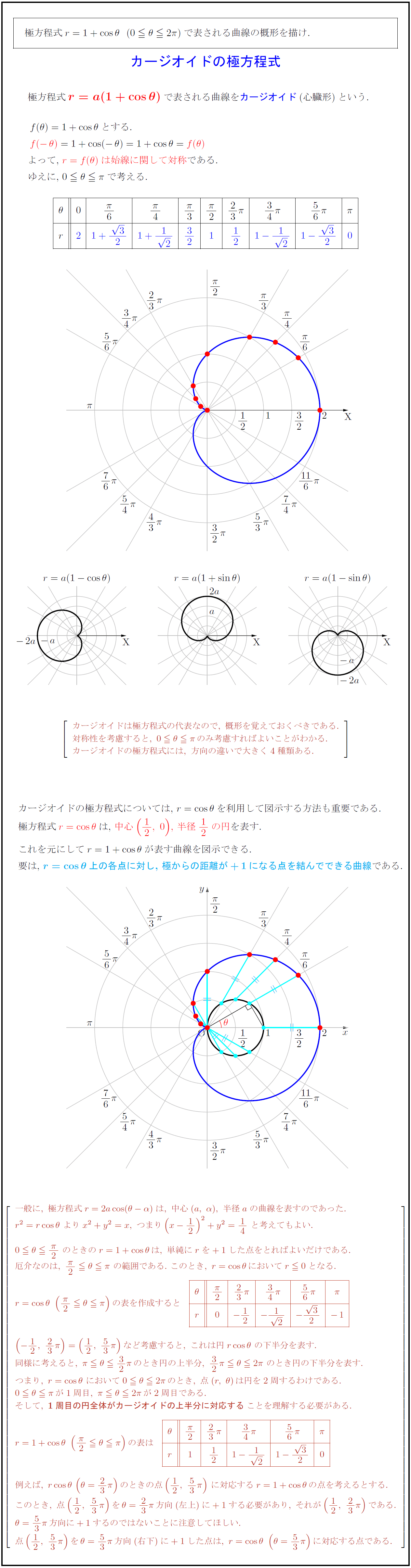
極方程式$r=1+cosθ(0θ2π)$で表される曲線の概形を描け. カージオイドの極方程式 極方程式 ${r=a(1+cosθ)$}で表される曲線をカージオイド(心臓形)という. よって,\ $r=f(θ)$は始線に関して対称}である. \ カージオイドは極方程式の代表なので,\ 概形を覚えておくべきである. 対称性を考慮すると,\ 0θπのみ考慮すればよいことがわかる. カージオイドの極方程式には,\ 方向の違いで大きく4種類ある. カージオイドの極方程式については,\ $r=cosθ$を利用して図示する方法も重要である. 極方程式$r=cosθ}$は,\ 中心$(12,\ 0)$,\ 半径$12$の円}を表す. これを元にして$r=1+cosθ$が表す曲線を図示できる. 要は,\ ${r=cosθ}$上の各点に対し,\ 極からの距離が${+1}$になる点を結んでできる曲線である. 一般に,\ 極方程式r=2acos(θ-α)は,\ 中心(a,\ α),\ 半径aの曲線を表すのであった. \と考えてもよい. 0θ{π}{2}\ のときのr=1+cosθは,\ 単純にrを+1した点をとればよいだけである. 厄介なのは,\ {π}{2}θπ\ の範囲である.\ このとき,\ r=cosθにおいてr0となる. の表を作成するとなど考慮すると,\ これは円rcosθ\ の下半分を表す. 同様に考えると,\ πθ32πのとき円の上半分,\ 32πθ2π\ のとき円の下半分を表す. つまり,\ r=cosθ\ において0θ2πのとき,\ 点(r,\ θ)は円を2周するわけである. 0θπが1周目,\ πθ2πが2周目である. そして,\ {1周目の円全体がカージオイドの上半分に対応する}ことを理解する必要がある. \方向に+1するのではないことに注意してほしい. 点(12,\ 53π)をθ=53π方向(右下)に+1した点は,\ r=cosθ\ (θ=53π)に対応する点である.

