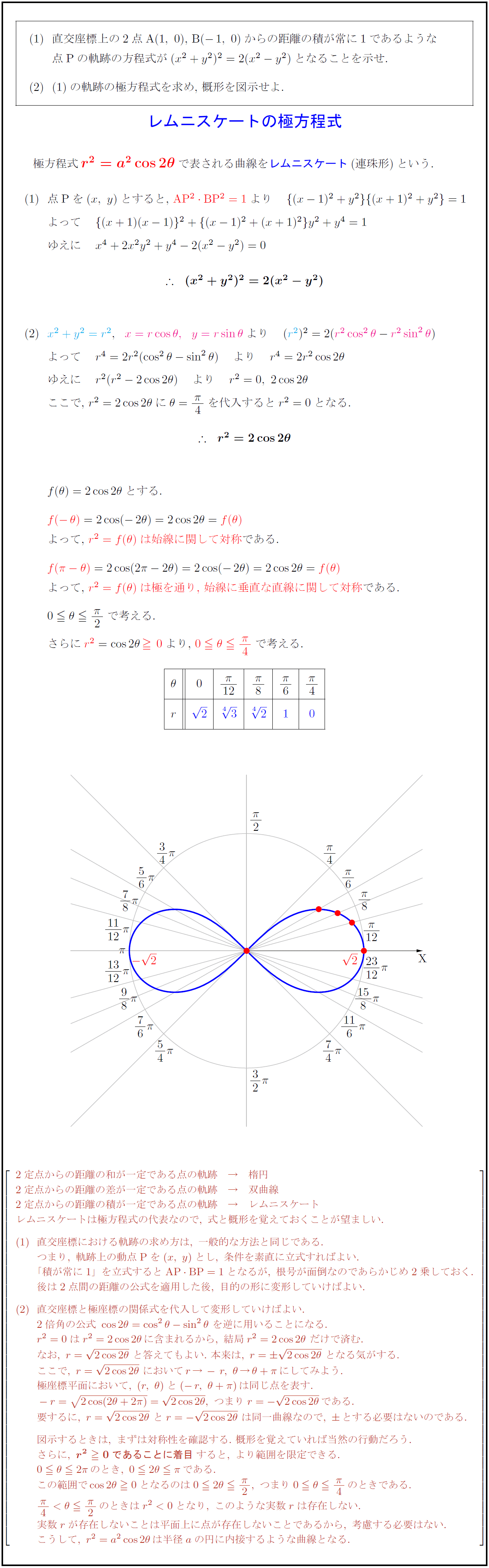
直交座標上の2点A$(1,\ 0)$,\ B($-1,\ 0$)からの距離の積が常に1であるような 点Pの軌跡の方程式が$(x²+y²)²=2(x²-y²)$となることを示せ. の軌跡の極方程式を求め,\ 概形を図示せよ. レムニスケートの極方程式 極方程式 ${r²=a²cos2θ$}で表される曲線をレムニスケート(連珠形)という. 始線に関して対称}であは極を通り,\ 始線に垂直な直線に関して対称}である. { }$0θ{π}{2}$で考える. 2定点からの距離の和が一定である点の軌跡 → 楕円 2定点からの距離の差が一定である点の軌跡 → 双曲線 2定点からの距離の積が一定である点の軌跡 → レムニスケート レムニスケートは極方程式の代表なので,\ 式と概形を覚えておくことが望ましい. 直交座標における軌跡の求め方は,\ 一般的な方法と同じである. つまり,\ 軌跡上の動点{P}を(x,\ y)とし,\ 条件を素直に立式すればよい. 「積が常に1」を立式すると{AP BP=1}となるが,\ 根号が面倒なのであらかじめ2乗しておく. 後は2点間の距離の公式を適用した後,\ 目的の形に変形していけばよい. 直交座標と極座標の関係式を代入して変形していけばよい. 2倍角の公式\ cos2θ=cos²θ-sin²θ\ を逆に用いることになる. r²=0はr²=2cos2θに含まれるから,\ 結局r²=2cos2θ\ だけで済む. なお,\ r={2cos2θ}\ と答えてもよい.\ 本来は,\ r={2cos2θ}\ となる気がする. ここで,\ r={2cos2θ}\ においてr→-r,\ θ→θ+πにしてみよう. 極座標平面において,\ (r,\ θ)と(-r,\ θ+π)は同じ点を表す. 要するに,\ r={2cos2θ}\ とr=-{2cos2θ}\ は同一曲線なので,\ とする必要はないのである. 図示するときは,\ まずは対称性を確認する.\ 概形を覚えていれば当然の行動だろう. さらに,\ {r²0であることに着目}すると,\ より範囲を限定できる. この範囲でcos2θ0となるのは02θ{π}{2},\ つまり0θ{π}{4}のときである. {π}{4}<θ{π}{2}のときはr²<0となり,\ このような実数rは存在しない. 実数rが存在しないことは平面上に点が存在しないことであるから,\ 考慮する必要はない. こうして,\ r²=a²cos2θは半径aの円に内接するような曲線となる.

