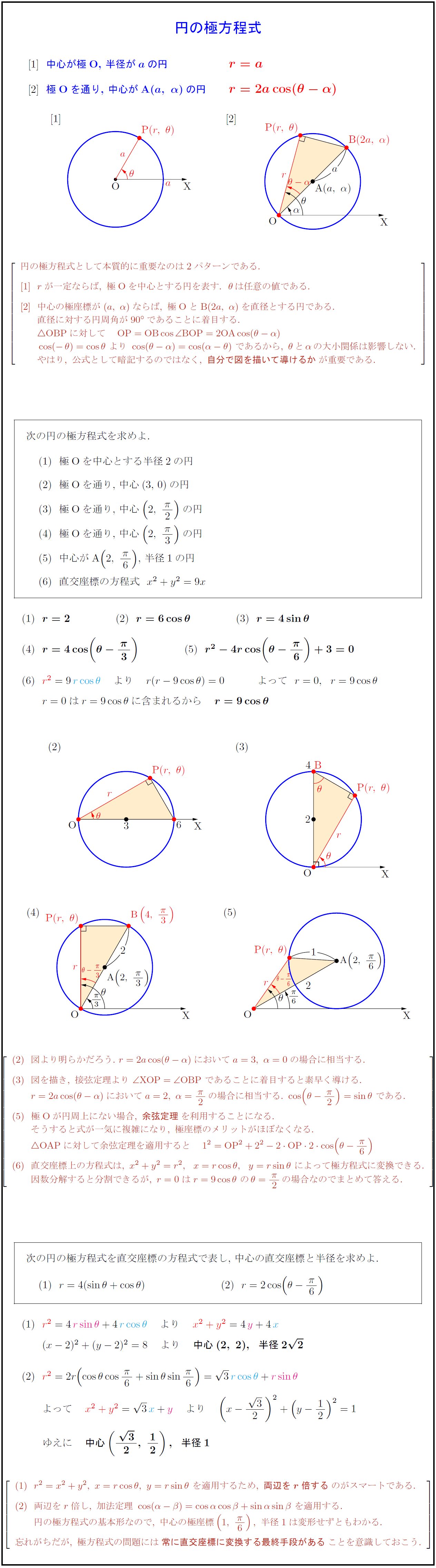
中心が極O,\ 半径が${a}$の円 & ${r=a$} 極Oを通り,\ 中心がA${(a,\ α)}$の円 円の極方程式として本質的に重要なのは2パターンである. rが一定ならば,\ 極 Oを中心とする円を表す.θは任意の値である. 中心の極座標が(a,\ α)ならば,\ 極 Oと B(2a,\ α)を直径とする円である. 直径に対する円周角が90°であることに着目する. {OBPに対して OP=OBcos∠ BOP=2OAcos(θ-α)} cos(-θ)=cosθ\ より\ cos(θ-α)=cos(α-θ)\ であるから,\ θとαの大小関係は影響しない. やはり,\ 公式として暗記するのではなく,\ {自分で図を描いて導けるか}が重要である. 次の円の極方程式を求めよ. 極Oを中心とする半径2の円 極Oを通り,\ 中心(3,\ 0)の円 極Oを通り,\ 中心$(2,\ {π}{2})$の円 極Oを通り,\ 中心$(2,\ {π}{3})$の円 中心がA$(2,\ {π}{6})$,\ 半径1の円 直交座標の方程式$x²+y²=9x$ 図より明らかだろう.\ r=2acos(θ-α)においてa=3,\ α=0の場合に相当する. 図を描き,\ 接弦定理より\ {∠ XOP=∠ OBP}\ であることに着目すると素早く導ける. r=2acos(θ-α)においてa=2,\ α={π}{2}の場合に相当する.\ cos(θ-{π}{2})=sinθ\ である. 極 Oが円周上にない場合,\ {余弦定理}を利用することになる. そうすると式が一気に複雑になり,\ 極座標のメリットがほぼなくなる. {OAP}に対して余弦定理を適用すると {1²=OP²+2²-2 OP2cos(θ-{π}{6})} 直交座標上の方程式は,\ x²+y²=r²,x=rcosθ,y=rsinθ\ によって極方程式に変換できる. 因数分解すると分割できるが,\ r=0はr=9cosθ\ のθ={π}{2}の場合なのでまとめて答える. 次の円の極方程式を直交座標の方程式で表し,\ 中心の直交座標と半径を求めよ. r²=x²+y²,\ x=rcosθ,\ y=rsinθ\ を適用するため,\ {両辺をr倍する}のがスマートである. 両辺をr倍し,\ 加法定理\ cos(α-β)=cosαcosβ+sinαsinβ\ を適用する. 円の極方程式の基本形なので,\ 中心の極座標(1,\ {π}{6}),\ 半径1は変形せずともわかる. 忘れがちだが,\ 極方程式の問題には{常に直交座標に変換する最終手段がある}ことを意識しておこう.


