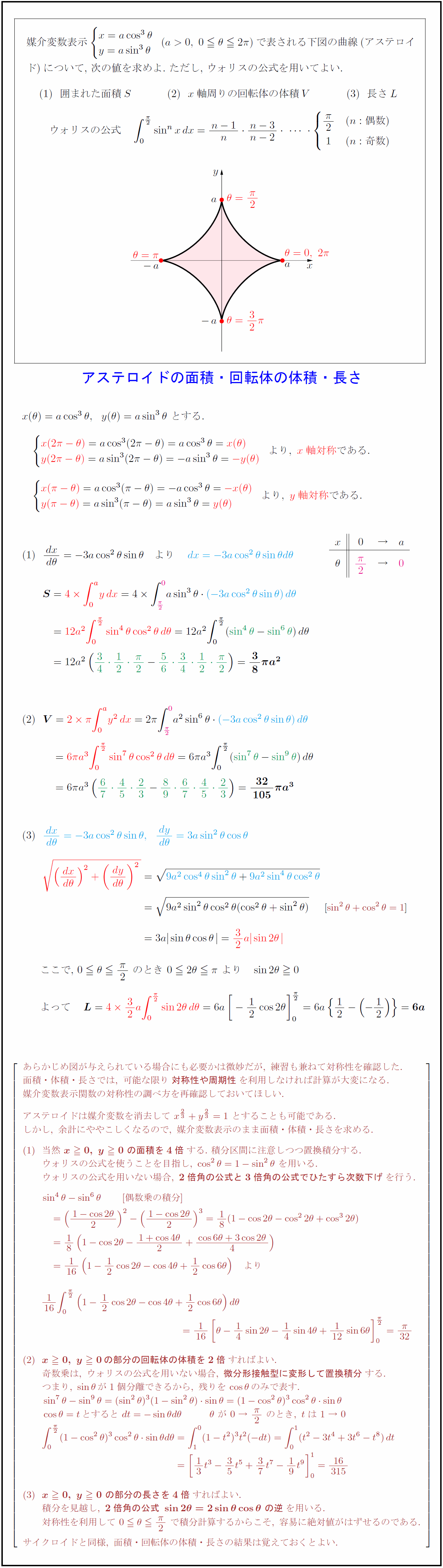
媒介変数表示$ x=acos³θ y=asin³θ -(a>0,\ 0θ2π)$で表される下図の曲線(アステロイ ド)について,\ 次の値を求めよ.\ ただし,\ ウォリスの公式を用いてよい. 囲まれた面積$S$ $x$軸周りの回転体の体積$V$ 長さ$L$ ウォリスの公式 {π}{2} & (n:偶数) \ 1 & (n:奇数) あらかじめ図が与えられている場合にも必要かは微妙だが,\ 練習も兼ねて対称性を確認した. 面積・体積・長さでは,\ 可能な限り{対称性や周期性}を利用しなければ計算が大変になる. 媒介変数表示関数の対称性の調べ方を再確認しておいてほしい. アステロイドは媒介変数を消去して\ x^{2/3}+y^{2/3}=1\ とすることも可能である. しかし,\ 余計にややこしくなるので,\ 媒介変数表示のまま面積・体積・長さを求める. 当然\ {x0,\ y0\ の面積を4倍}する.\ 積分区間に注意しつつ置換積分する. ウォリスの公式を使うことを目指し,\ cos²θ=1-sin²θ\ を用いる. ウォリスの公式を用いない場合,\ {2倍角の公式と3倍角の公式でひたすら次数下げ}を行う. sin⁴θ-sin^6θ [偶数乗の積分] {x0,\ y0の部分の回転体の体積を2倍}すればよい. 奇数乗は,\ ウォリスの公式を用いない場合,\ {微分形接触型に変形して置換積分}する. つまり,\ sinθが1個分離できるから,\ 残りをcosθのみで表す. {x0,\ y0\ の部分の長さを4倍}すればよい. 積分を見越し,\ {2倍角の公式\ sin2θ=2sinθcosθ\ の逆}を用いる. 対称性を利用して\ 0θ{π}{2}\ で積分計算するからこそ,\ 容易に絶対値がはずせるのである. サイクロイドと同様,\ 面積・回転体の体積・長さの結果は覚えておくとよい.

