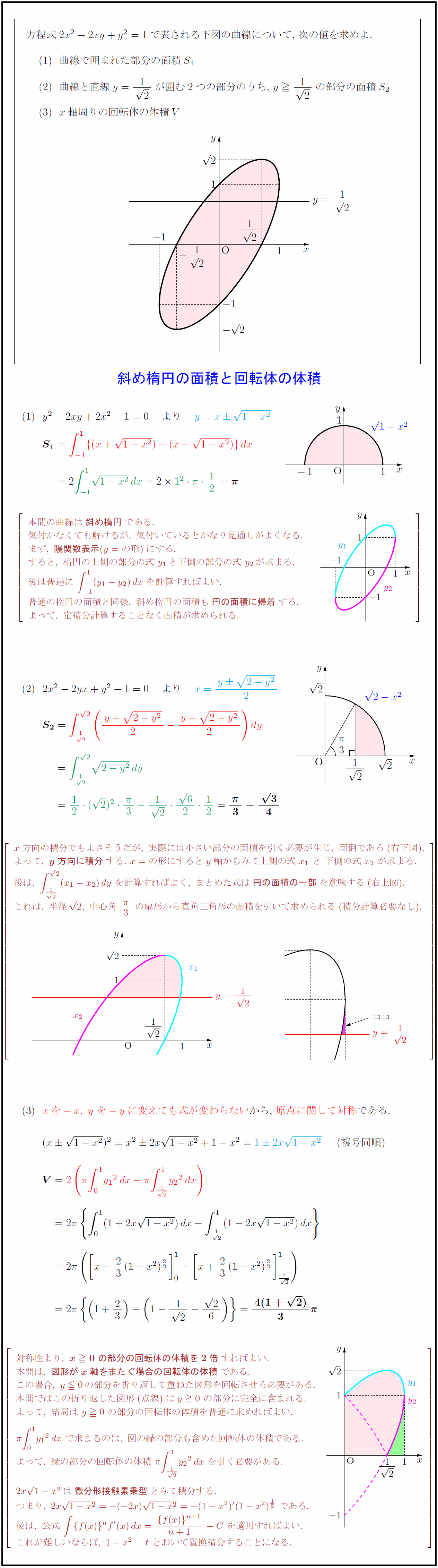
方程式$2x²-2xy+y²=1$で表される下図の曲線について,\ 次の値を求めよ. 曲線で囲まれた部分の面積$S₁$ 曲線と直線$y={1}{2}$が囲む2つの部分のうち,\ $y{1}{2}$の部分の面積$S₂$ $x$軸周りの回転体の体積$V$ 本問の曲線は{斜め楕円}である. 気付かなくても解けるが,\ 気付いているとかなり見通しがよくなる. まず,\ {陽関数表示}(y=の形)にする. すると,\ 楕円の上側の部分の式\ y₁と下側の部分の式\ y₂が求まる. 後は普通に\ ∫-1}{1}(y₁-y₂)dx\ を計算すればよい. 普通の楕円の面積と同様,\ 斜め楕円の面積も{円の面積に帰着}する. よって,\ 定積分計算することなく面積が求められる. x方向の積分でもよさそうだが,\ 実際には小さい部分の面積を引く必要が生じ,\ 面倒である(右下図). よって,\ {y方向に積分}する.\ x=の形にするとy軸からみて上側の式\ x₁\ と\ 下側の式\ x₂\ が求まる. 後は,\ ∫1}{2{2}(x₁-x₂)dy\ を計算すればよく,\ まとめた式は{円の面積の一部}を意味する(右上図). [1.3zh] これは,\ 半径2,\ 中心角\ {π}{3}\ の扇形から直角三角形の面積を引いて求められる(積分計算必要なし). $xを-x,\ yを-y$に変えても式が変わらない}から,\ 原点に関して対称}である. 対称性より,\ {x0\ の部分の回転体の体積を2倍}すればよい. 本問は,\ {図形がx軸をまたぐ場合の回転体の体積}である. この場合,\ y0の部分を折り返して重ねた図形を回転させる必要がある. 本問ではこの折り返した図形(点線)はy0\ の部分に完全に含まれる. よって,\ 結局は\ y0\ の部分の回転体の体積を普通に求めればよい. π∫{y₁}²dx\ で求まるのは,\ 図の緑の部分も含めた回転体の体積である. よって,\ 緑の部分の回転体の体積\ π∫1}{2{1}{y₂}²dx\ を引く必要がある. 2x{1-x²}は{微分形接触累乗型}とみて積分する. つまり,\ 2x{1-x²}=-(-2x){1-x²}=-(1-x²)'(1-x²)^{1/2}\ である. 後は,\ 公式\ ∫{f(x)}^nf'(x)dx=f(x)}^{n+1{n+1}+C\ を適用すればよい. これが難しいならば,\ 1-x²=t\ とおいて置換積分することになる.

