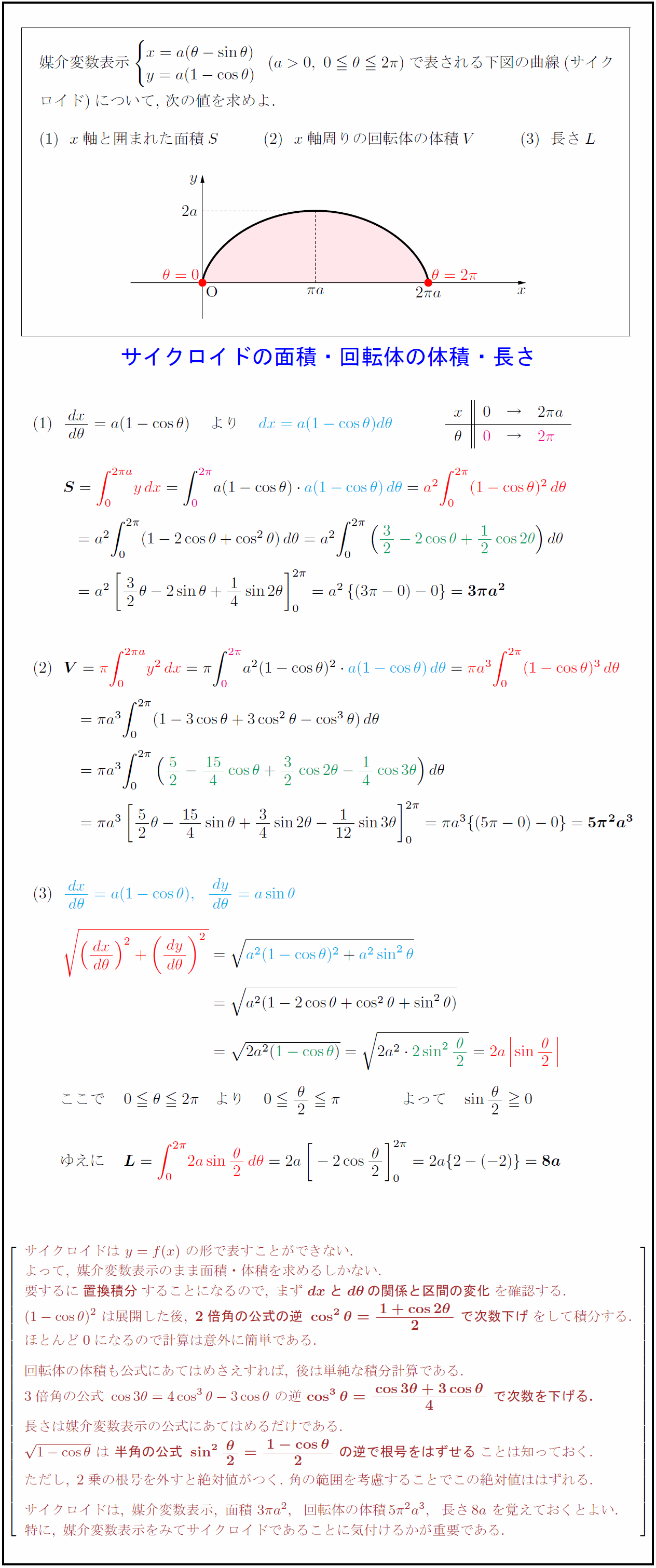
媒介変数表示$ x=a(θ-sinθ) y=a(1-cosθ) -(a>0,\ 0θ2π)$で表される下図の曲線(サイク ロイド)について,\ 次の値を求めよ. $x$軸と囲まれた面積$S$ $x$軸周りの回転体の体積$V$ 長さ$L$ サイクロイドは\ y=f(x)\ の形で表すことができない. よって,\ 媒介変数表示のまま面積・体積を求めるしかない. 要するに{置換積分}することになるので,\ まず{dxとdθの関係と区間の変化}を確認する. (1-cosθ)²\ は展開した後,\ {2倍角の公式の逆\ cos²θ={1+cos2θ}{2}\ で次数下げ}をして積分する. ほとんど0になるので計算は意外に簡単である. 回転体の体積も公式にあてはめさえすれば,\ 後は単純な積分計算である. 3倍角の公式\ cos3θ=4cos³θ-3cosθ\ の逆\ {cos³θ={cos3θ+3cosθ}{4}\ で次数を下げる.} 長さは媒介変数表示の公式にあてはめるだけである. {1-cosθ}\ は\ {半角の公式\ sin²{θ}{2}={1-cosθ}{2}\ の逆で根号をはずせる}ことは知っておく. ただし,\ 2乗の根号を外すと絶対値がつく.\ 角の範囲を考慮することでこの絶対値ははずれる. サイクロイドは,\ 媒介変数表示,\ 面積\ 3π a²,回転体の体積5π²a³,長さ8a\ を覚えておくとよい. 特に,\ 媒介変数表示をみてサイクロイドであることに気付けるかが重要である.

