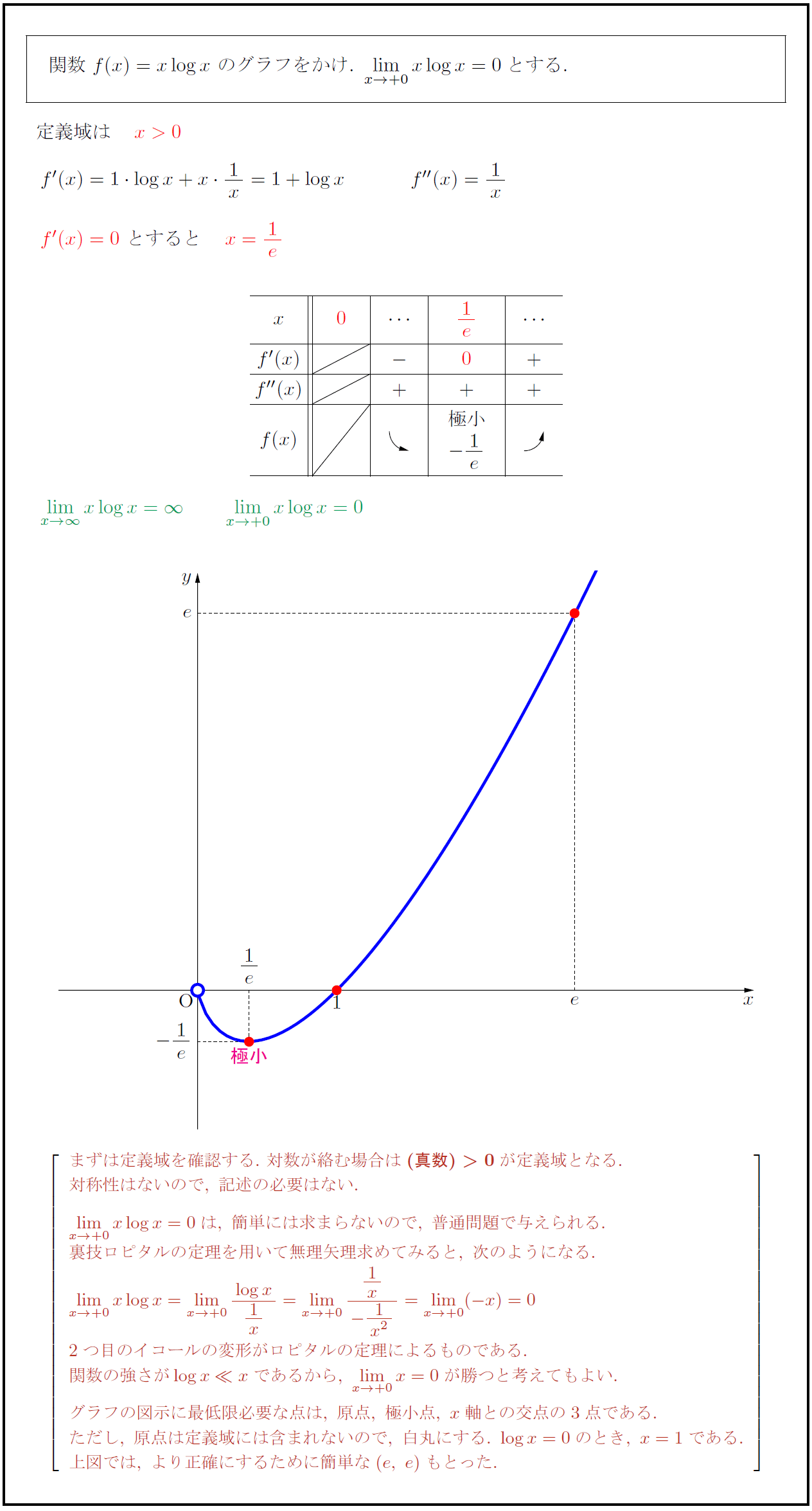
まずは定義域を確認する.\ 対数が絡む場合は{(真数)>0}が定義域となる. 対称性はないので,\ 記述の必要はない. limx→+0}xlog x=0は,\ 簡単には求まらないので,\ 普通問題で与えられる. 裏技ロピタルの定理を用いて無理矢理求めてみると,\ 次のようになる. limx→+0}xlog x=limx→+0}{log x}{1x}=limx→+0}{1x}{-{1}{x²=limx→+0}(-x)=0 [1.8zh] 2つ目のイコールの変形がロピタルの定理によるものである. 関数の強さがlog x\ll xであるから,\ limx→+0}x=0が勝つと考えてもよい. グラフの図示に最低限必要な点は,\ 原点,\ 極小点,\ x軸との交点の3点である. ただし,\ 原点は定義域には含まれないので,\ 白丸にする.\ log x=0のとき,\ x=1である. 上図では,\ より正確にするために簡単な(e,\ e)もとった.

