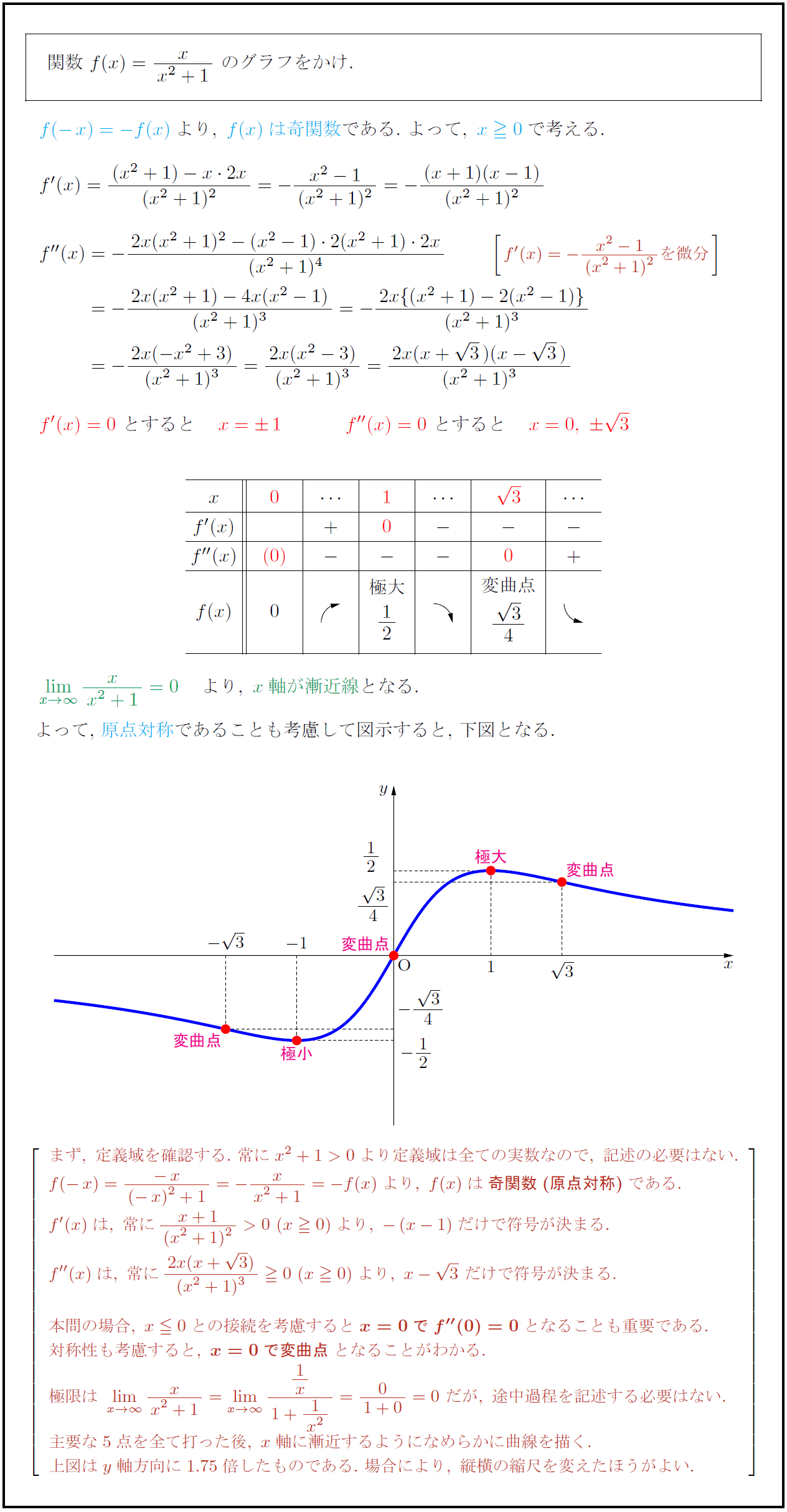
$関数\ f(x)={x}{x²+1}\ のグラフをかけ.$ は奇関数}であを微分{x軸が漸近線}となる.$ よって,\ 原点対称}であることも考慮して図示すると,\ 下図となる. 極大} \B[ne]{変曲点} \C[s]{極小} \D[sw]{変曲点} まず,\ 定義域を確認する.\ 常にx²+1>0より定義域は全ての実数なので,\ 記述の必要はない. f(-x)={-x}{(-x)²+1}=-{x}{x²+1}=-f(x)より,\ f(x)は{奇関数(原点対称)}である. f'(x)は,\ 常に{x+1}{(x²+1)²}>0\ (x0)より,\ -(x-1)だけで符号が決まる. f”(x)は,\ 常に{2x(x+3)}{(x²+1)³}0\ (x0)より,\ x-3\ だけで符号が決まる. 本問の場合,\ x0との接続を考慮すると{x=0でf”(0)=0}となることも重要である. 対称性も考慮すると,\ {x=0で変曲点}となることがわかる. 極限は\ lim[x→∞]{x}{x²+1}=lim[x→∞]{1x}{1+{1}{x²={0}{1+0}=0\ だが,\ 途中過程を記述する必要はない. 主要な5点を全て打った後,\ x軸に漸近するようになめらかに曲線を描く. 上図はy軸方向に1.75倍したものである.\ 場合により,\ 縦横の縮尺を変えたほうがよい.

