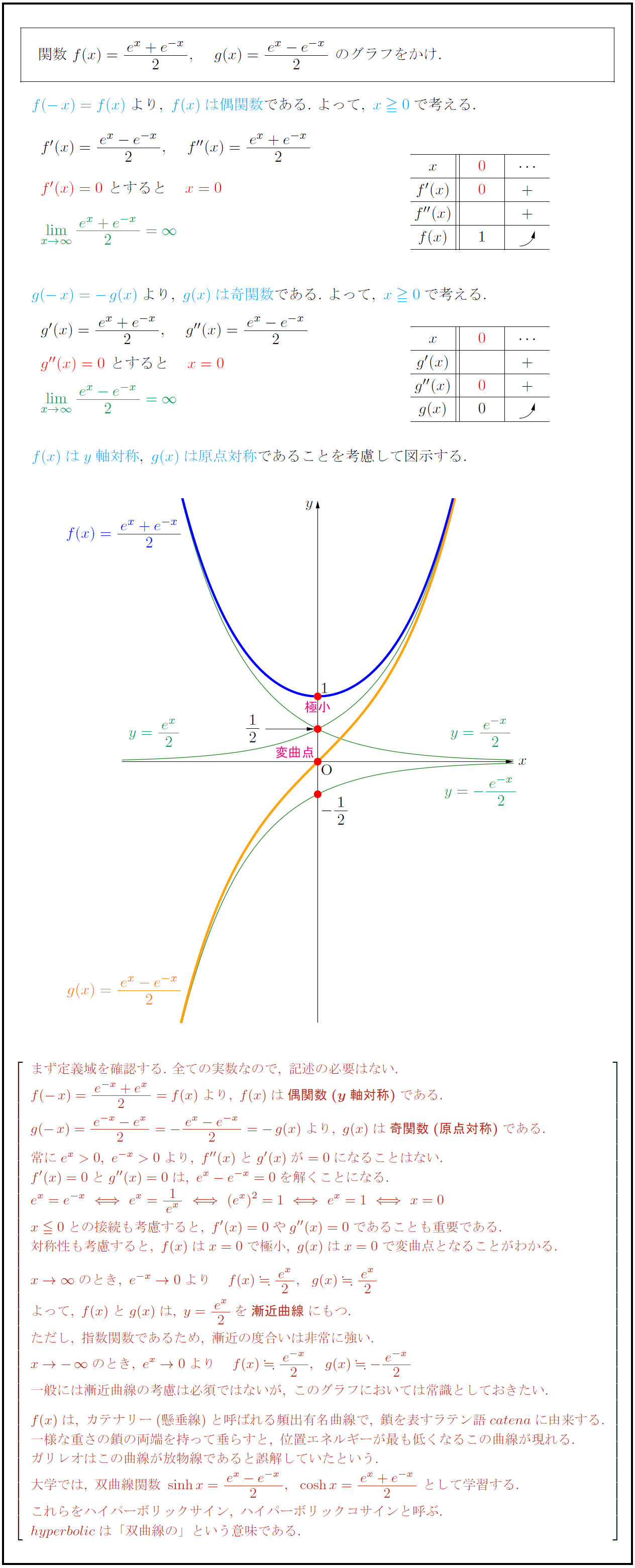
まず定義域を確認する.\ 全ての実数なので,\ 記述の必要はない. f(-x)={e^{-x}+e^x}{2}=f(x)より,\ f(x)は{偶関数(y軸対称)}である. g(-x)={e^{-x}-e^x}{2}=-{e^x-e^{-x{2}=-g(x)より,\ g(x)は{奇関数(原点対称)}である. 常にe^x>0,\ e^{-x}>0より,\ f”(x)とg'(x)が=0になることはない. f'(x)=0とg”(x)=0は,\ e^x-e^{-x}=0を解くことになる. e^x=e^{-x}e^x={1}{e^x}(e^x)²=1e^x=1x=0 x0との接続も考慮すると,\ f'(x)=0やg”(x)=0であることも重要である. 対称性も考慮すると,\ f(x)はx=0で極小,\ g(x)はx=0で変曲点となることがわかる. x→∞ のとき,\ e^{-x}→0より f(x){e^x}{2},g(x){e^x}{2} よって,\ f(x)とg(x)は,\ y={e^x}{2}を{漸近曲線}にもつ. ただし,\ 指数関数であるため,\ 漸近の度合いは非常に強い. x→-∞ のとき,\ e^x→0より f(x){e^{-x{2},g(x)-{e^{-x{2} 一般には漸近曲線の考慮は必須ではないが,\ このグラフにおいては常識としておきたい. f(x)は,\ カテナリー(懸垂線)と呼ばれる頻出有名曲線で,\ 鎖を表すラテン語catenaに由来する. 一様な重さの鎖の両端を持って垂らすと,\ 位置エネルギーが最も低くなるこの曲線が現れる. ガリレオはこの曲線が放物線であると誤解していたという. 大学では,\ 双曲線関数\ sinh x={e^x-e^{-x{2},cosh x={e^x+e^{-x{2}\ として学習する. これらをハイパーボリックサイン,\ ハイパーボリックコサインと呼ぶ. hyperbolicは「双曲線の」という意味である.

