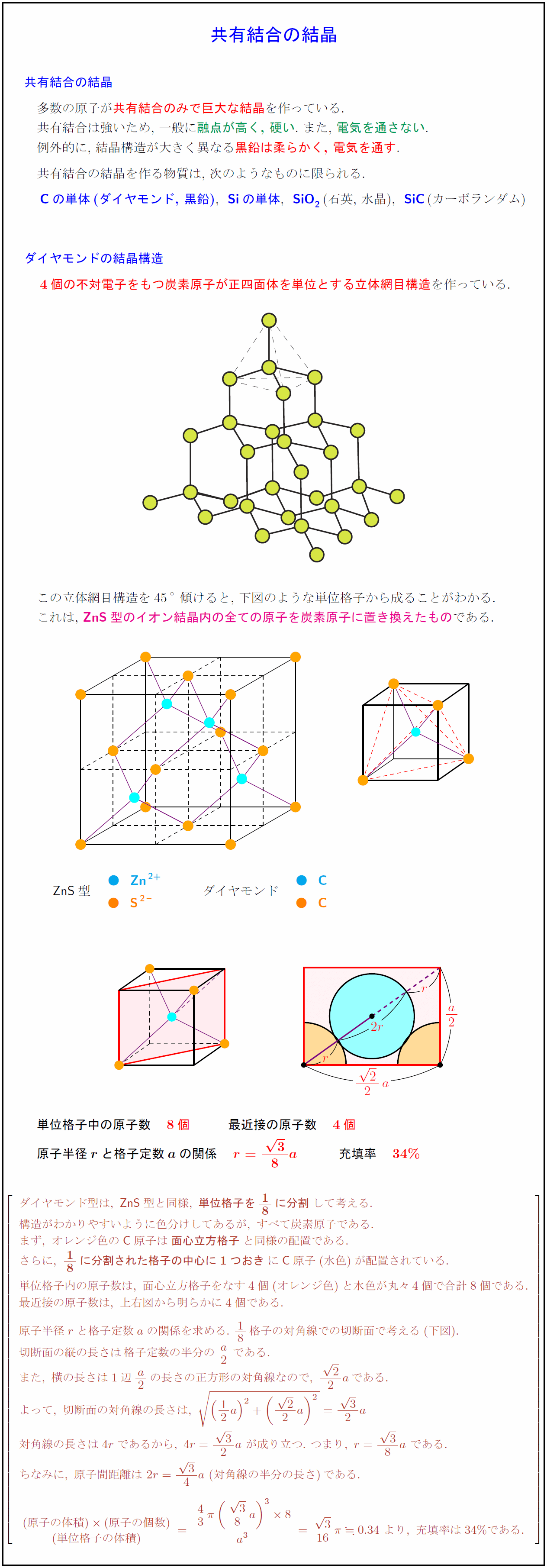
多数の原子が共有結合のみで巨大な結晶を作っている. 共有結合は強いため,\ 一般に融点が高く,\ 硬い.\ また,\ 電気を通さない. 例外的に,\ 結晶構造が大きく異なる黒鉛は柔らかく,\ 電気を通す. 共有結合の結晶を作る物質は,\ 次のようなものに限られる. {C}の単体(ダイヤモンド,\ 黒鉛),{Si}の単体,{SiO₂}(石英,\ 水晶),{SiC}(カーボランダム) ダイヤモンドの結晶構造 4個の不対電子をもつ炭素原子が正四面体を単位とする立体網目構造を作っている. この立体網目構造を45°傾けると,\ 下図のような単位格子から成ることがわかる. これは,\ {ZnS}型のイオン結晶内の全ての原子を炭素原子に置き換えたものである. [-1.5zh] 単位格子中の原子数 8個} 最近接の原子数 4個 原子半径${r}$と格子定数${a}$の関係 充填率 ダイヤモンド型は,\ {ZnS}型と同様,\ {単位格子を1/8に分割}して考える. 構造がわかりやすいように色分けしてあるが,\ すべて炭素原子である. まず,\ オレンジ色の{C}原子は{面心立方格子}と同様の配置である. さらに,\ {1/8に分割された格子の中心に1つおき}に{C}原子(水色)が配置されている. 単位格子内の原子数は,\ 面心立方格子をなす4個(オレンジ色)と水色が丸々4個で合計8個である. 最近接の原子数は,\ 上右図から明らかに4個である. 原子半径rと格子定数aの関係を求める.\ 1/8格子の対角線での切断面で考える(下図). 切断面の縦の長さは格子定数の半分の a2である. また,\ 横の長さは1辺 a2の長さの正方形の対角線なので,\ {2}{2}aである. よって,\ 切断面の対角線の長さは,\ 対角線の長さは4rであるから,\ 4r={3}{2}a\ が成り立つ.\ つまり,\ r={3}{8}a\ である. ちなみに,\ 原子間距離は\ 2r={3}{4}a\ (対角線の半分の長さ)である. {(原子の体積)(原子の個数)}{(単位格子の体積)}kinzi0.34\ より,\ 充填率は34\%である.

