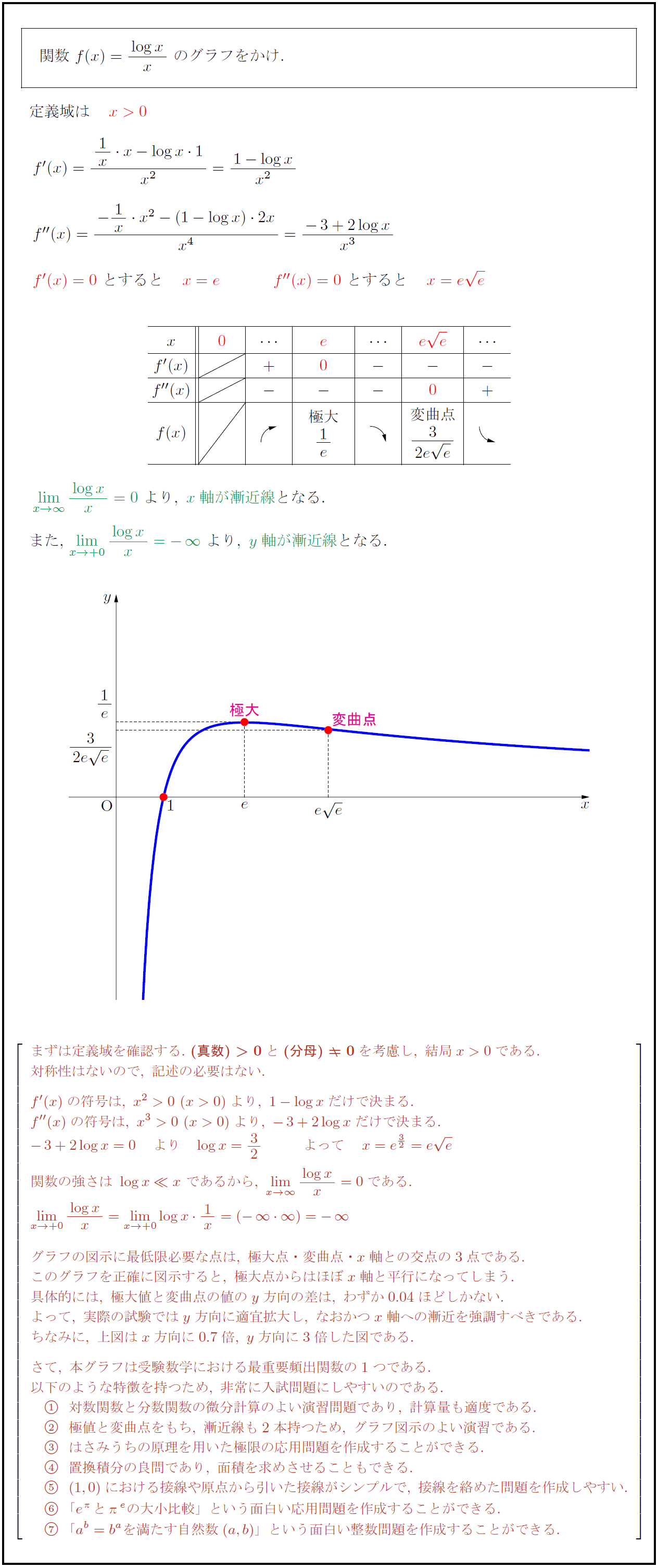
まずは定義域を確認する.\ {(真数)>0}と{(分母)0}を考慮し,\ 結局x>0である. 対称性はないので,\ 記述の必要はない. f'(x)の符号は,\ x²>0\ (x>0)より,\ 1-log xだけで決まる. f”(x)の符号は,\ x³>0\ (x>0)より,\ -3+2log xだけで決まる. -3+2log x=0 より log x=32 よって x=e^{3/2}=e e 関数の強さは\ log x\ll x\ であるから,\ lim[x→∞]{log x}{x}=0である. グラフの図示に最低限必要な点は,\ 極大点・変曲点・x軸との交点の3点である. このグラフを正確に図示すると,\ 極大点からはほぼx軸と平行になってしまう. 具体的には,\ 極大値と変曲点の値のy方向の差は,\ わずか0.04ほどしかない. よって,\ 実際の試験ではy方向に適宜拡大し,\ なおかつx軸への漸近を強調すべきである. ちなみに,\ 上図はx方向に0.7倍,\ y方向に3倍した図である. さて,\ 本グラフは受験数学における最重要頻出関数の1つである. 以下のような特徴を持つため,\ 非常に入試問題にしやすいのである. 対数関数と分数関数の微分計算のよい演習問題であり,\ 計算量も適度である. 極値と変曲点をもち,\ 漸近線も2本持つため,\ グラフ図示のよい演習である. はさみうちの原理を用いた極限の応用問題を作成することができる. 置換積分の良問であり,\ 面積を求めさせることもできる. (1,0)における接線や原点から引いた接線がシンプルで,\ 接線を絡めた問題を作成しやすい. ⑥「e^πとπ^eの大小比較」という面白い応用問題を作成することができる. ⑦「a^b=b^aを満たす自然数(a,b)」という面白い整数問題を作成することができる.

