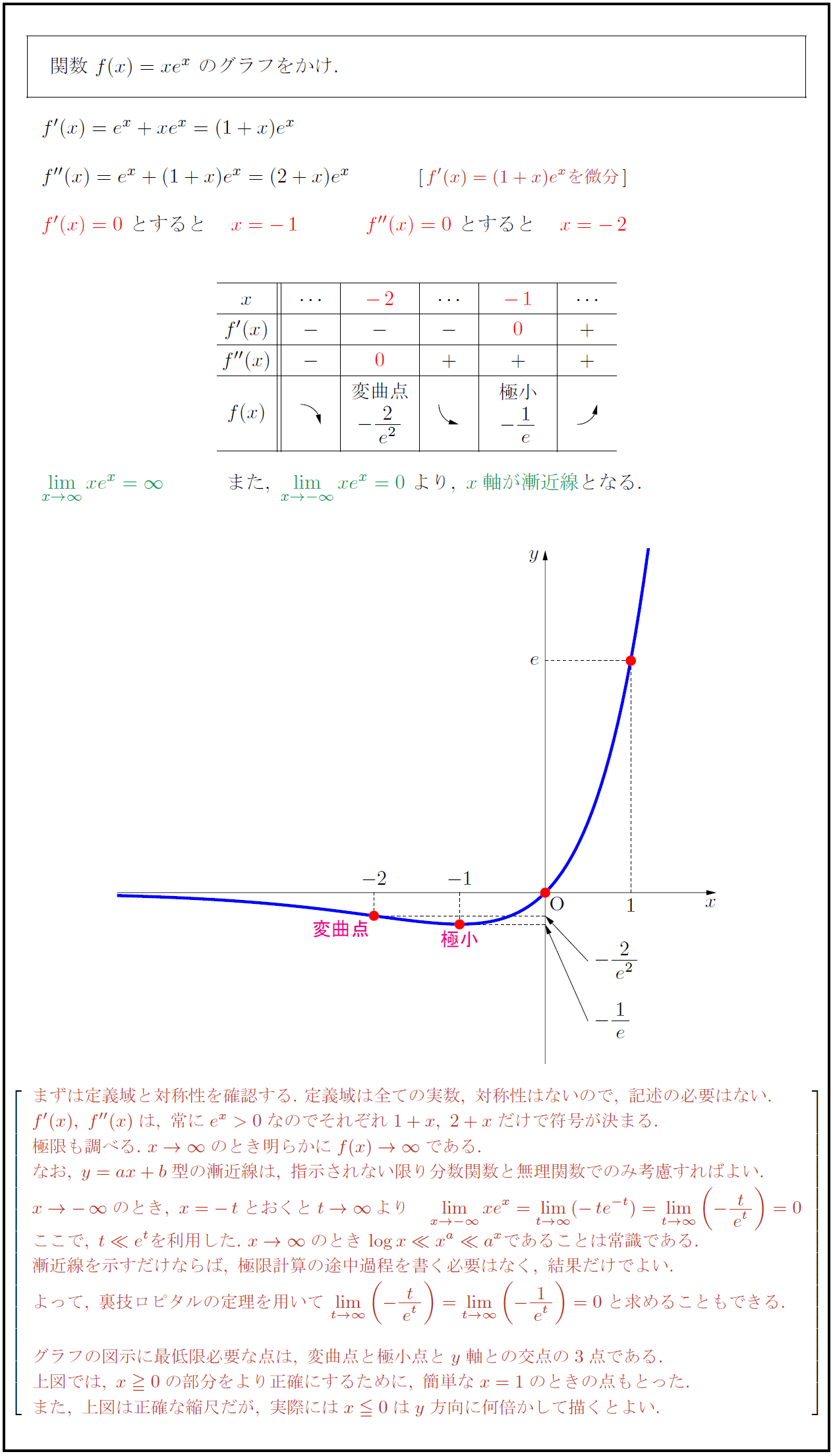
まずは定義域と対称性を確認する.\ 定義域は全ての実数,\ 対称性はないので,\ 記述の必要はない. f'(x),\ f”(x)は,\ 常にe^x>0なのでそれぞれ1+x,\ 2+xだけで符号が決まる. 極限も調べる.\ x→∞ のとき明らかにf(x)→∞ である. なお,\ y=ax+b型の漸近線は,\ 指示されない限り分数関数と無理関数でのみ考慮すればよい. ここで,\ t\ll e^tを利用した.\ x→∞ のときlog x\ll x^a\ll a^xであることは常識である. 漸近線を示すだけならば,\ 極限計算の途中過程を書く必要はなく,\ 結果だけでよい. よって,\ 裏技ロピタルの定理を用いてlimt→∞}(-{t}{e^t})=limt→∞}(-{1}{e^t})=0と求めることもできる. グラフの図示に最低限必要な点は,\ 変曲点と極小点とy軸との交点の3点である. 上図では,\ x0の部分をより正確にするために,\ 簡単なx=1のときの点もとった. また,\ 上図は正確な縮尺だが,\ 実際にはx0はy方向に何倍かして描くとよい.

