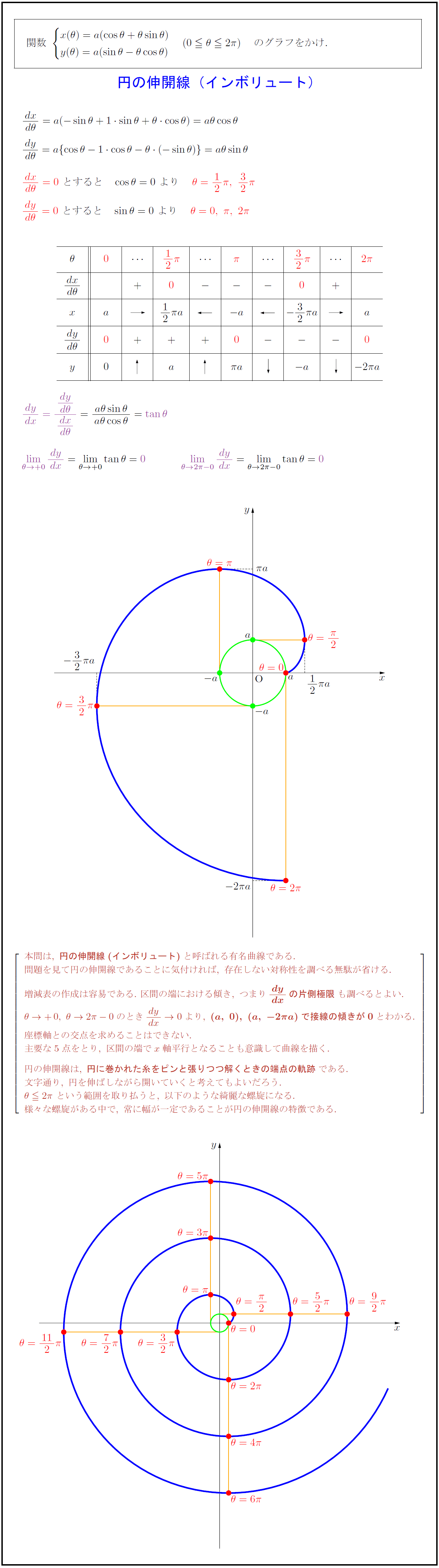
本問は,\ {円の伸開線(インボリュート)}と呼ばれる有名曲線である. 問題を見て円の伸開線であることに気付ければ,\ 存在しない対称性を調べる無駄が省ける. 増減表の作成は容易である.\ 区間の端における傾き,\ つまりdy}{dx}の片側極限}も調べるとよい. θ→+0,\ θ→2π-0のとき{dy}{dx}→0より,\ {(a,\ 0),\ (a,\ -2π a)で接線の傾きが0}とわかる. 座標軸との交点を求めることはできない. 主要な5点をとり,\ 区間の端でx軸平行となることも意識して曲線を描く. 円の伸開線は,\ {円に巻かれた糸をピンと張りつつ解くときの端点の軌跡}である. 文字通り,\ 円を伸ばしながら開いていくと考えてもよいだろう. θ2π\ という範囲を取り払うと,\ 以下のような綺麗な螺旋になる. 様々な螺旋がある中で,\ 常に幅が一定であることが円の伸開線の特徴である.

