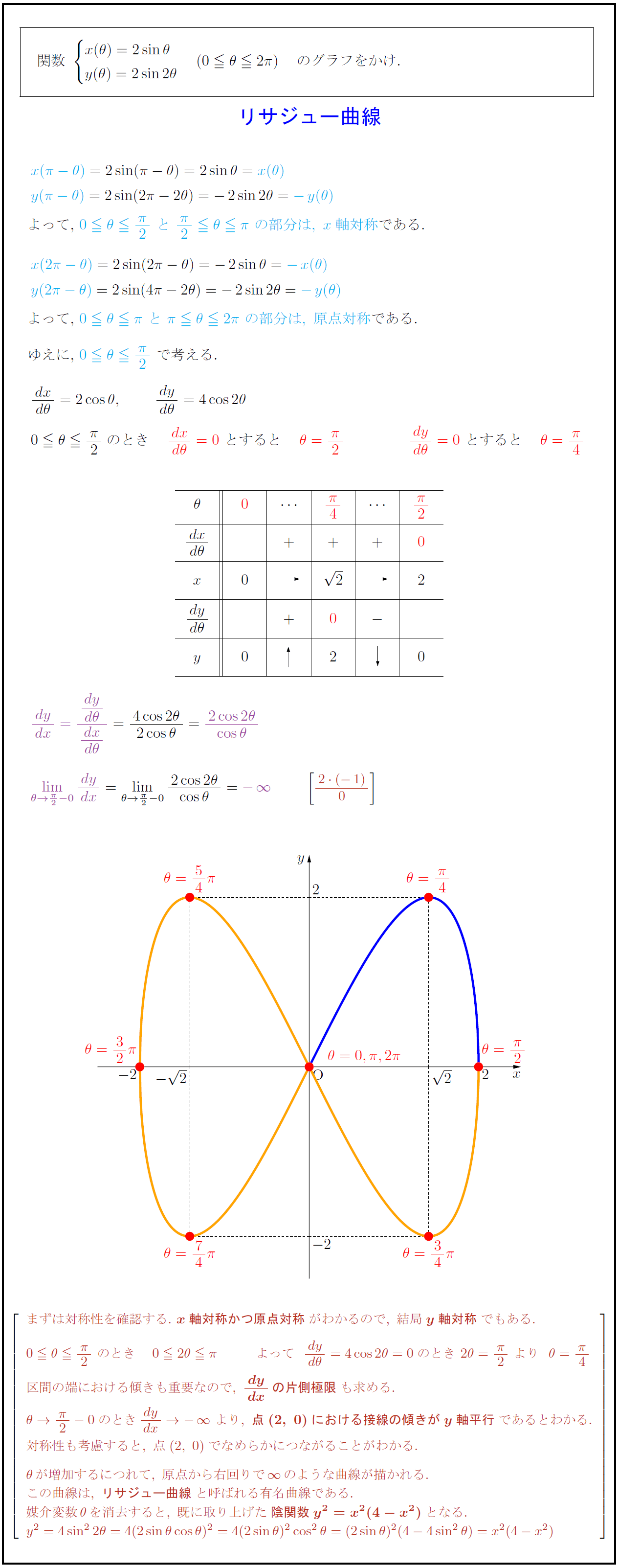
まずは対称性を確認する.\ {x軸対称かつ原点対称}がわかるので,\ 結局{y軸対称}でもある. 0θ{π}{2}\ のとき 02θπ よって{dy}{dθ}=4cos2θ=0のとき\ 2θ={π}{2}\ よりθ={π}{4} 区間の端における傾きも重要なので,\ dy}{dx}の片側極限}も求める. θ→{π}{2}-0のとき{dy}{dx}→-∞\ より,\ {点(2,\ 0)における接線の傾きがy軸平行}であるとわかる. 対称性も考慮すると,\ 点(2,\ 0)でなめらかにつながることがわかる. θが増加するにつれて,\ 原点から右回りで∞のような曲線が描かれる. この曲線は,\ {リサジュー曲線}と呼ばれる有名曲線である. 媒介変数θを消去すると,\ 既に取り上げた{陰関数y²=x²(4-x²)}となる. \

