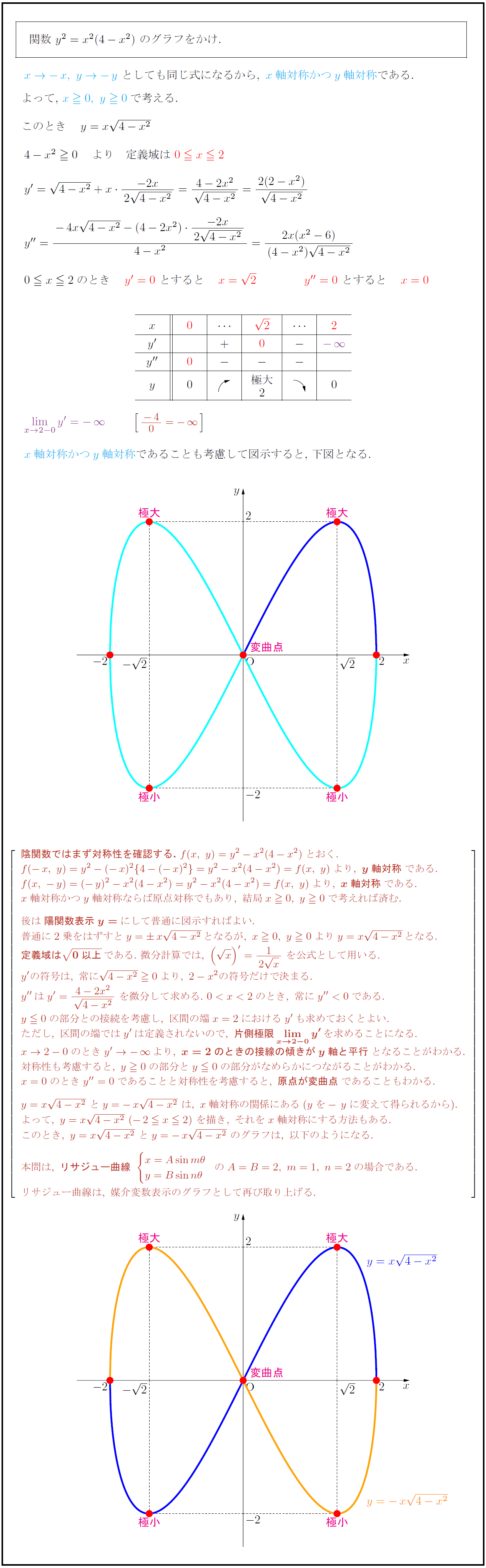
陰関数ではまず対称性を確認する.}\ f(x,\ y)=y²-x²(4-x²)とおく. f(-x,\ y)=y²-(-x)²{4-(-x)²}=y²-x²(4-x²)=f(x,\ y)より,\ {y軸対称}である. f(x,\ -y)=(-y)²-x²(4-x²)=y²-x²(4-x²)=f(x,\ y)より,\ {x軸対称}である. x軸対称かつy軸対称ならば原点対称でもあり,\ 結局x0,\ y0で考えれば済む. 後は{陽関数表示y=}にして普通に図示すればよい. 普通に2乗をはずすとy=x{4-x²}となるが,\ x0,\ y0よりy=x{4-x²}となる. {定義域は{0以上である.\ 微分計算では,\ ( x)’={1}{2 x}\ を公式として用いる. y’の符号は,\ 常に{4-x²}0より,\ 2-x²の符号だけで決まる. y”はy’={4-2x²}4-x²\ を微分して求める.常にy”<0である.="" y0の部分との接続を考慮し,\="" 区間の端x="2におけるy'も求めておくとよい." ただし,\="" 区間の端ではy'は定義されないので,\="" {片側極限limx→2-0}y'}を求めることになる.="" x→2-0のときy'→-∞より,\="" {x="2のときの接線の傾きがy軸と平行}となることがわかる." 対称性も考慮すると,\="" y0の部分とy0の部分がなめらかにつながることがわかる.="" x="0のときy''=0であることと対称性を考慮すると,\" {原点が変曲点}であることもわかる.="" y="x{4-x²}\" とy="-x{4-x²}\" は,\="" x軸対称の関係にある(yを-yに変えて得られるから).="" よって,\="" (-2="" x2)\="" を描き,\="" それをx軸対称にする方法もある.="" このとき,\="" のグラフは,\="" 以下のようになる.="" 本問は,\="" {リサジュー曲線}\="" mθ="" nθ="" -のa="B=2,\" m="1,\" n="2の場合である." ₀="" リサジュー曲線は,\="" 媒介変数表示のグラフとして再び取り上げる.

