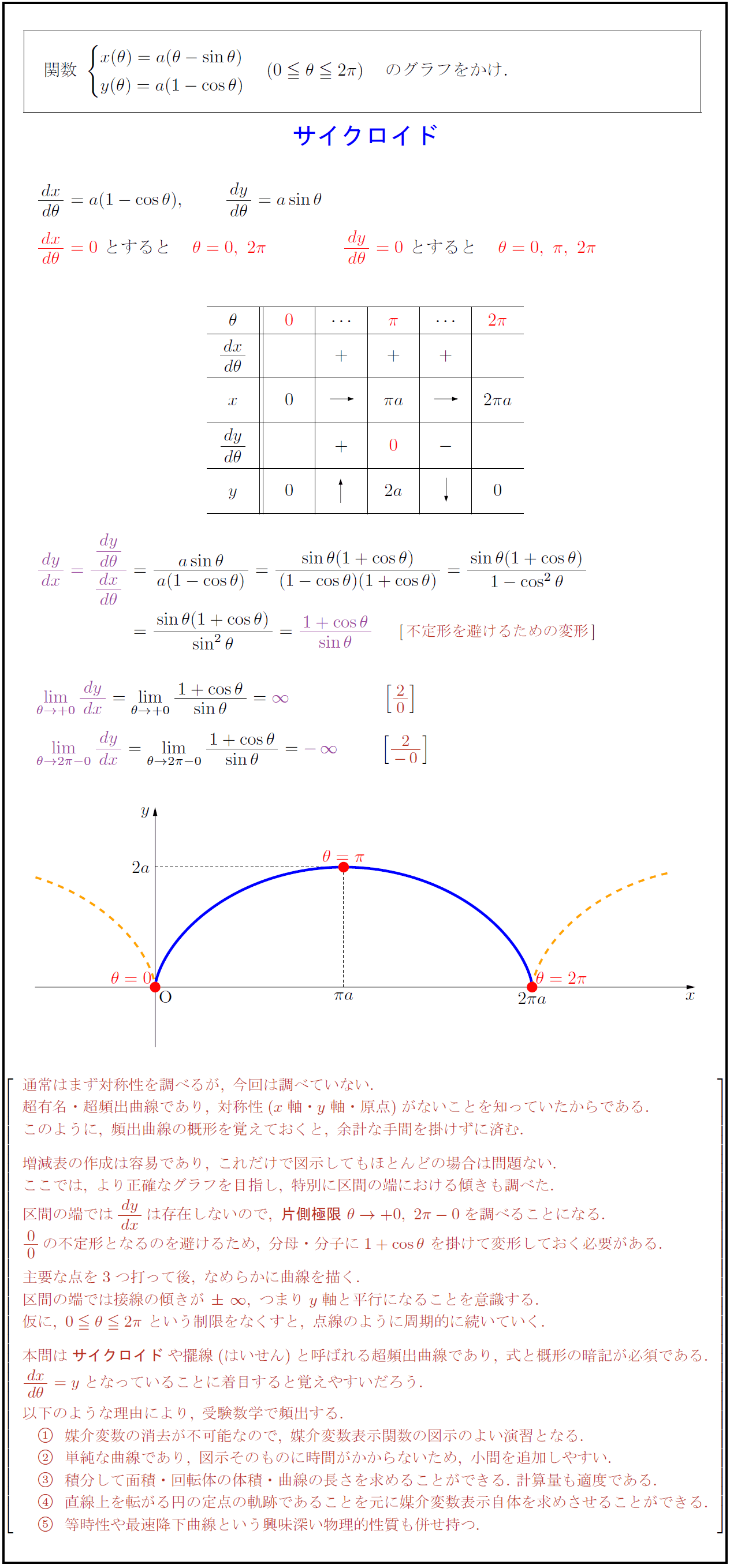
通常はまず対称性を調べるが,\ 今回は調べていない. 超有名・超頻出曲線であり,\ 対称性(x軸・y軸・原点)がないことを知っていたからである. このように,\ 頻出曲線の概形を覚えておくと,\ 余計な手間を掛けずに済む. 増減表の作成は容易であり,\ これだけで図示してもほとんどの場合は問題ない. ここでは,\ より正確なグラフを目指し,\ 特別に区間の端における傾きも調べた. 区間の端では{dy}{dx}は存在しないので,\ {片側極限}\ θ→+0,\ 2π-0を調べることになる. 00の不定形となるのを避けるため,\ 分母・分子に1+cosθ\ を掛けて変形しておく必要がある. 主要な点を3つ打って後,\ なめらかに曲線を描く. 区間の端では接線の傾きが∞,\ つまりy軸と平行になることを意識する. 仮に,\ 0θ2π\ という制限をなくすと,\ 点線のように周期的に続いていく. 本問は{サイクロイド}や擺線(はいせん)と呼ばれる超頻出曲線であり,\ 式と概形の暗記が必須である. {dx}{dθ}=yとなっていることに着目すると覚えやすいだろう. 以下のような理由により,\ 受験数学で頻出する. 媒介変数の消去が不可能なので,\ 媒介変数表示関数の図示のよい演習となる. 単純な曲線であり,\ 図示そのものに時間がかからないため,\ 小問を追加しやすい. 積分して面積・回転体の体積・曲線の長さを求めることができる.\ 計算量も適度である. 直線上を転がる円の定点の軌跡であることを元に媒介変数表示自体を求めさせることができる. 等時性や最速降下曲線という興味深い物理的性質も併せ持つ.

