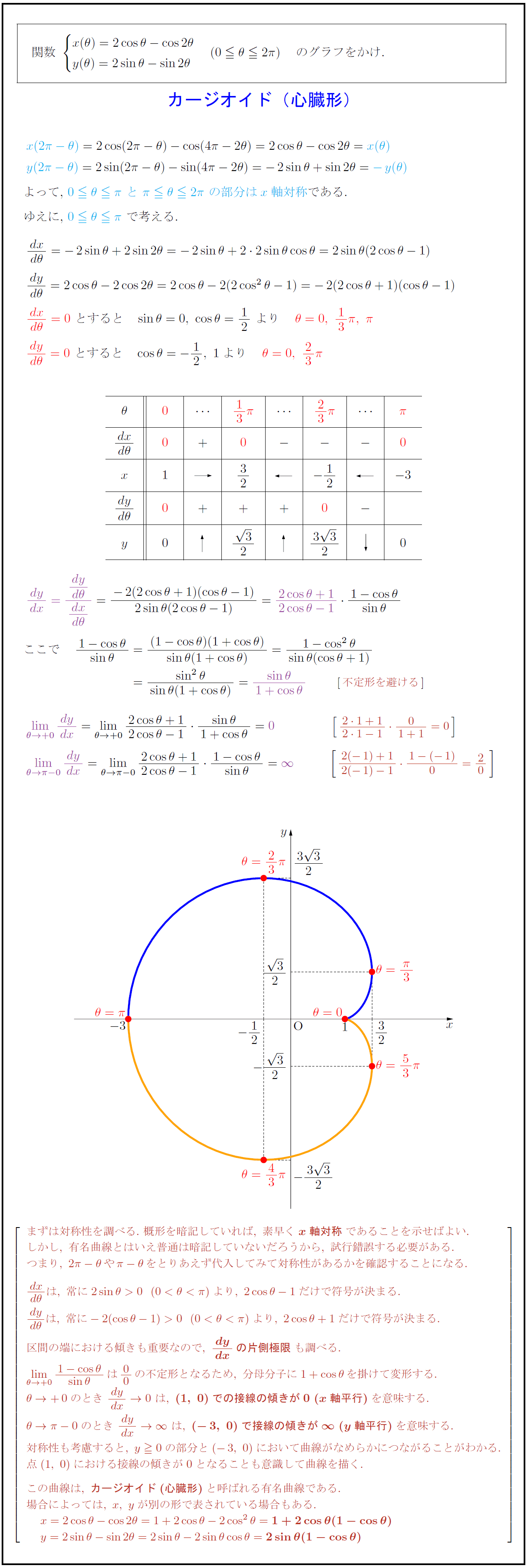
まずは対称性を調べる.\ 概形を暗記していれば,\ 素早く{x軸対称}であることを示せばよい. しかし,\ 有名曲線とはいえ普通は暗記していないだろうから,\ 試行錯誤する必要がある. つまり,\ 2π-θやπ-θをとりあえず代入してみて対称性があるかを確認することになる. {dx}{dθ}は,\ 常に2sinθ>0(0<θ<π)より,\ 2cosθ-1だけで符号が決まる. {dy}{dθ}は,\ 常に-2(cosθ-1)>0(0<θ<π)より,\ 2cosθ+1だけで符号が決まる. 区間の端における傾きも重要なので,\ dy}{dx}の片側極限}も調べる. limθ→+0}{1-cosθ}{sinθ}は{0}{0}の不定形となるため,\ 分母分子に1+cosθを掛けて変形する. θ→+0のとき\ {dy}{dx}→0\ は,\ {(1,\ 0)での接線の傾きが0\ (x軸平行)}を意味する. θ→π-0のとき\ {dy}{dx}→∞\ は,\ {(-3,\ 0)で接線の傾きが∞\ (y軸平行)}を意味する. 対称性も考慮すると,\ y0の部分と(-3,\ 0)において曲線がなめらかにつながることがわかる. 点(1,\ 0)における接線の傾きが0となることも意識して曲線を描く. この曲線は,\ {カージオイド(心臓形)}と呼ばれる有名曲線である. 場合によっては,\ x,\ yが別の形で表されている場合もある.

