a>0と考えてください。
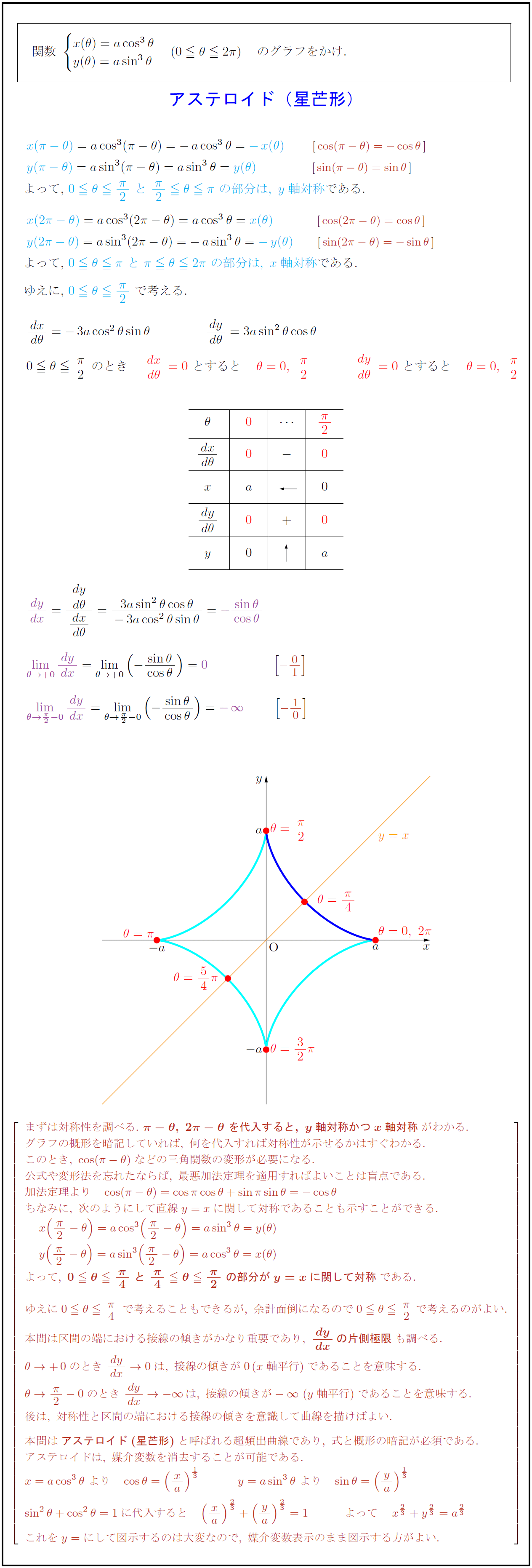
まずは対称性を調べる.\ {π-θ,\ 2π-θ\ を代入すると,\ y軸対称かつx軸対称}がわかる. グラフの概形を暗記していれば,\ 何を代入すれば対称性が示せるかはすぐわかる. このとき,\ cos(π-θ)などの三角関数の変形が必要になる. 公式や変形法を忘れたならば,\ 最悪加法定理を適用すればよいことは盲点である. 加法定理より cos(π-θ)=cosπcosθ+sinπsinθ=-cosθ ちなみに,\ 次のようにして直線y=xに関して対称であることも示すことができる. よって,\ {0θ{π}{4}\ と\ {π}{4}θ{π}{2}\ の部分がy=xに関して対称}である. ゆえに0θ{π}{4}\ で考えることもできるが,\ 余計面倒になるので0θ{π}{2}で考えるのがよい. 本問は区間の端における接線の傾きがかなり重要であり,\ dy}{dx}の片側極限}も調べる. θ→+0のとき\ {dy}{dx}→0は,\ 接線の傾きが0(x軸平行)であることを意味する. θ→{π}{2}-0のとき\ {dy}{dx}→-∞は,\ 接線の傾きが-∞\ (y軸平行)であることを意味する. 後は,\ 対称性と区間の端における接線の傾きを意識して曲線を描けばよい. 本問は{アステロイド(星芒形)}と呼ばれる超頻出曲線であり,\ 式と概形の暗記が必須である. アステロイドは,\ 媒介変数を消去することが可能である. これをy=にして図示するのは大変なので,\ 媒介変数表示のまま図示する方がよい.

