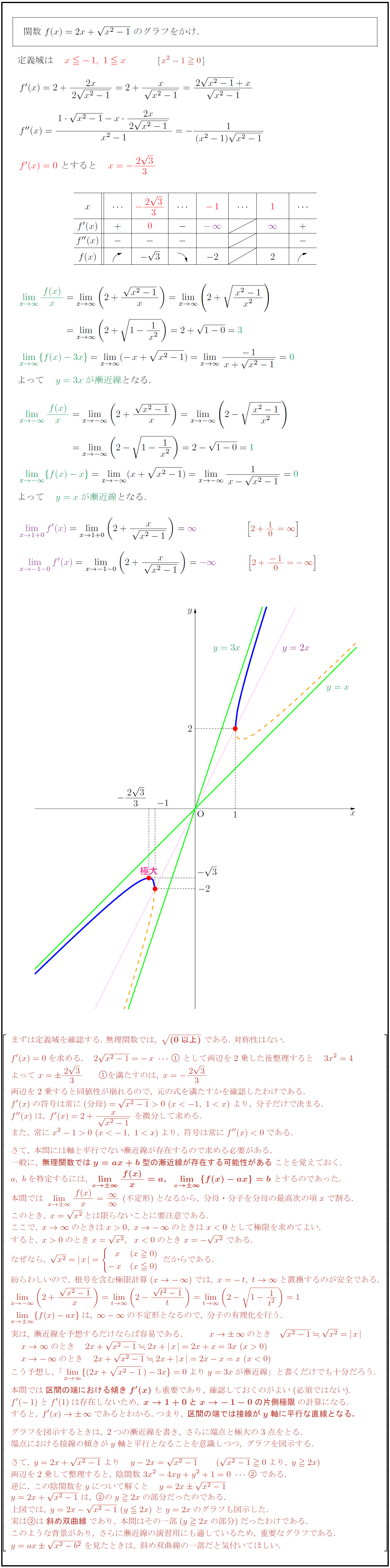
まずは定義域を確認する.\ 無理関数では,\ (0以上)\ である.\ 対称性はない. f'(x)=0を求める. 2{x²-1}=-x\ \ として両辺を2乗した後整理すると 3x²=4 よって\ x={23}{3} を満たすのは,\ x=-{23}{3} 両辺を2乗すると同値性が崩れるので,\ 元の式を満たすかを確認したわけである. f'(x)の符号は常に(分母)={x²-1}>0\ (x<-1,\ 10\ (x<-1,\ 10,\ x→-∞ のときはx<0として極限を求めてよい. すると,\ x>0のときx={x²},x<0のときx=-{x²}\ である. なぜなら,\ {x²}= x= {-}x & (x0) -x & (x0) \ だからである. ₀ 紛らわしいので,\ 根号を含む極限計算(x→-∞)では,\ x=-t,\ t→∞ と置換するのが安全である. limx→-∞-∞ の不定形となるので,\ 分子の有理化を行う. 実は,\ 漸近線を予想するだけならば容易である. こう予想し,\ 「lim[x→∞]{(2x+{x²-1})-3x}=0よりy=3xが漸近線」と書くだけでも十分だろう. 本問では{区間の端における傾きf'(x)}も重要であり,\ 確認しておくのがよい(必須ではない). f'(-1)とf'は存在しないため,\ {x→1+0とx→-1-0の片側極限}の計算になる. すると,\ f'(x)→∞ であるとわかる.\ つまり,\ {区間の端では接線がy軸に平行な直線となる.} グラフを図示するときは,\ 2つの漸近線を書き,\ さらに端点と極大の3点をとる. 端点における接線の傾きがy軸と平行となることを意識しつつ,\ グラフを図示する. さて,\ y=2x+{x²-1}\ より y-2x={x²-1} ({x²-1}0より,\ y 2x) 両辺を2乗して整理すると,\ 陰関数\ 3x²-4xy+y²+1=0\ \ である. 逆に,\ この陰関数をyについて解くと y=2x{x²-1} y=2x+{x²-1}\ は,\ のy 2xの部分だったのである. 上図では,\ y=2x-{x²-1}\ (y 2x)\ とy=2xのグラフも図示した. 実はは{斜め双曲線}であり,\ 本問はその一部(y2xの部分)だったわけである. このような背景があり,\ さらに漸近線の演習用にも適しているため,\ 重要なグラフである. y=ax{x²-b²}\ を見たときは,\ 斜め双曲線の一部だと気付いてほしい.

