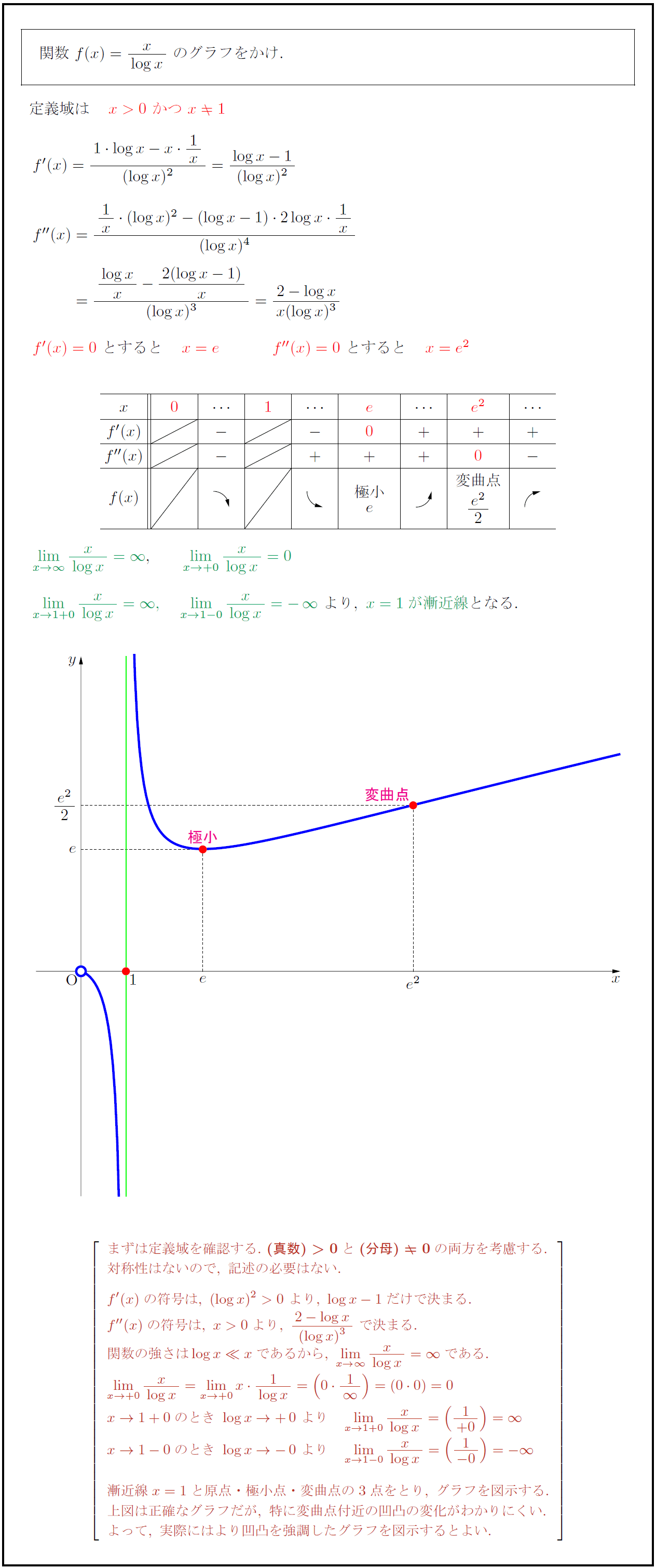
まずは定義域を確認する.\ {(真数)>0}と{(分母)0}の両方を考慮する. 対称性はないので,\ 記述の必要はない. f'(x)の符号は,\ (log x)²>0\ より,\ log x-1だけで決まる. f”(x)の符号は,\ x>0より,\ {2-log x}{(log x)³}\ で決まる. 関数の強さはlog x\ll xであるから,\ lim[x→∞]{x}{log x}=∞ である. limx→+0}{x}{log x}=limx→ +0}x{1}{log x}=(0{1}{∞})=(00)=0 x→1+0のとき\ log x→+0\ より limx→1+0}{x}{log x}=({1}{+0})=∞ x→1-0のとき\ log x→-0\ より limx→1-0}{x}{log x}=({1}{-0})=-∞ 漸近線x=1と原点・極小点・変曲点の3点をとり,\ グラフを図示する. 上図は正確なグラフだが,\ 特に変曲点付近の凹凸の変化がわかりにくい. よって,\ 実際にはより凹凸を強調したグラフを図示するとよい.

