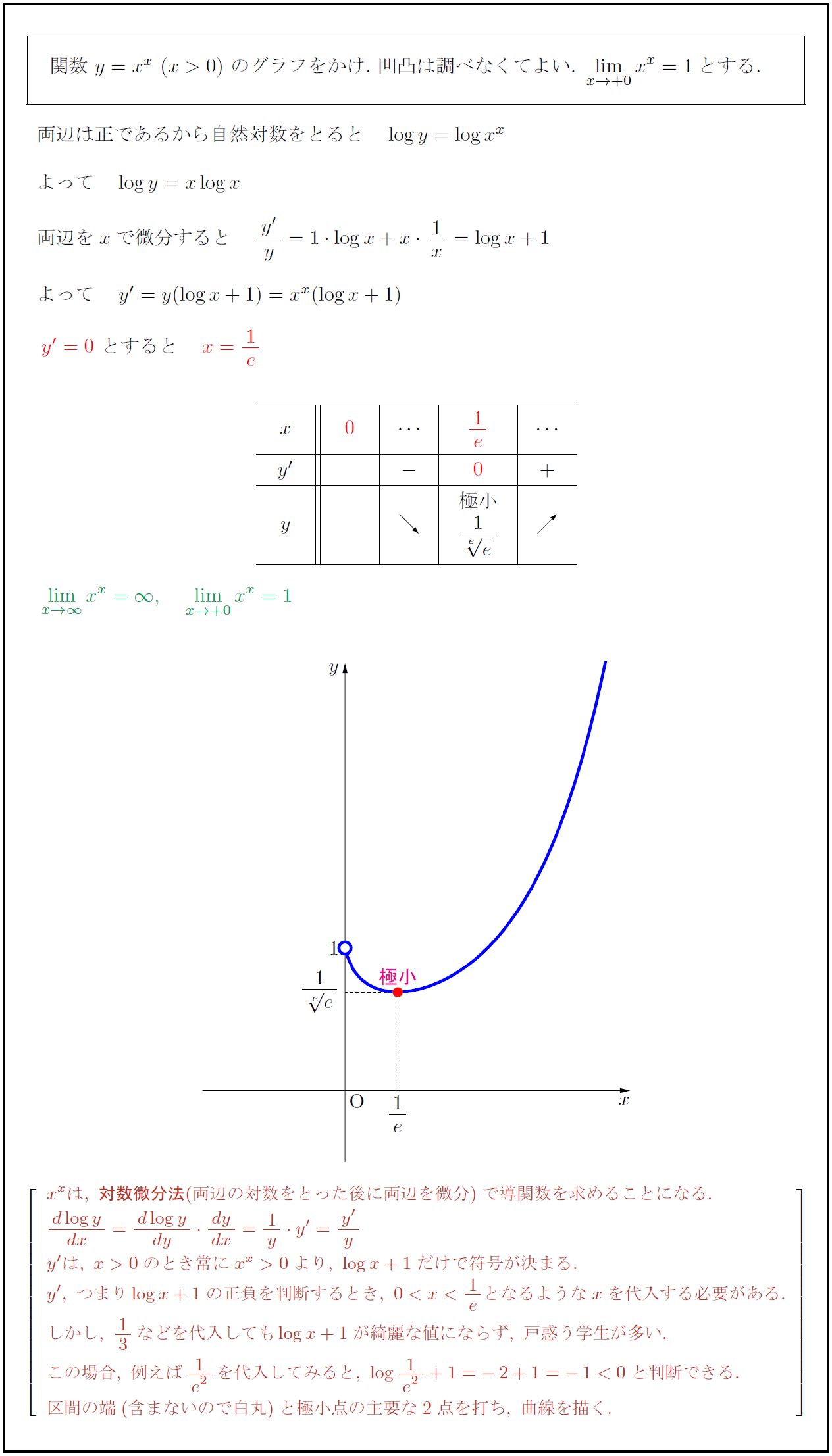
x^xは,\ {対数微分法}(両辺の対数をとった後に両辺を微分)で導関数を求めることになる. {dlog y}{dx}={dlog y}{dy}{dy}{dx}=1y y’={y’}{y} y’は,\ x>0のとき常にx^x>0より,\ log x+1だけで符号が決まる. y’,\ つまりlog x+1の正負を判断するとき,\ 0x1eとなるようなxを代入する必要がある. しかし,\=”” 13などを代入してもlog=”” x+1が綺麗な値にならず,\=”” 戸惑う学生が多い.=”” この場合,\=”” 例えば{1}{e²}を代入してみると,\=”” log{1}{e²}+1=”-2+1=-1<0と判断できる.” 区間の端(含まないので白丸)と極小点の主要な2点を打ち,\=”” 曲線を描

