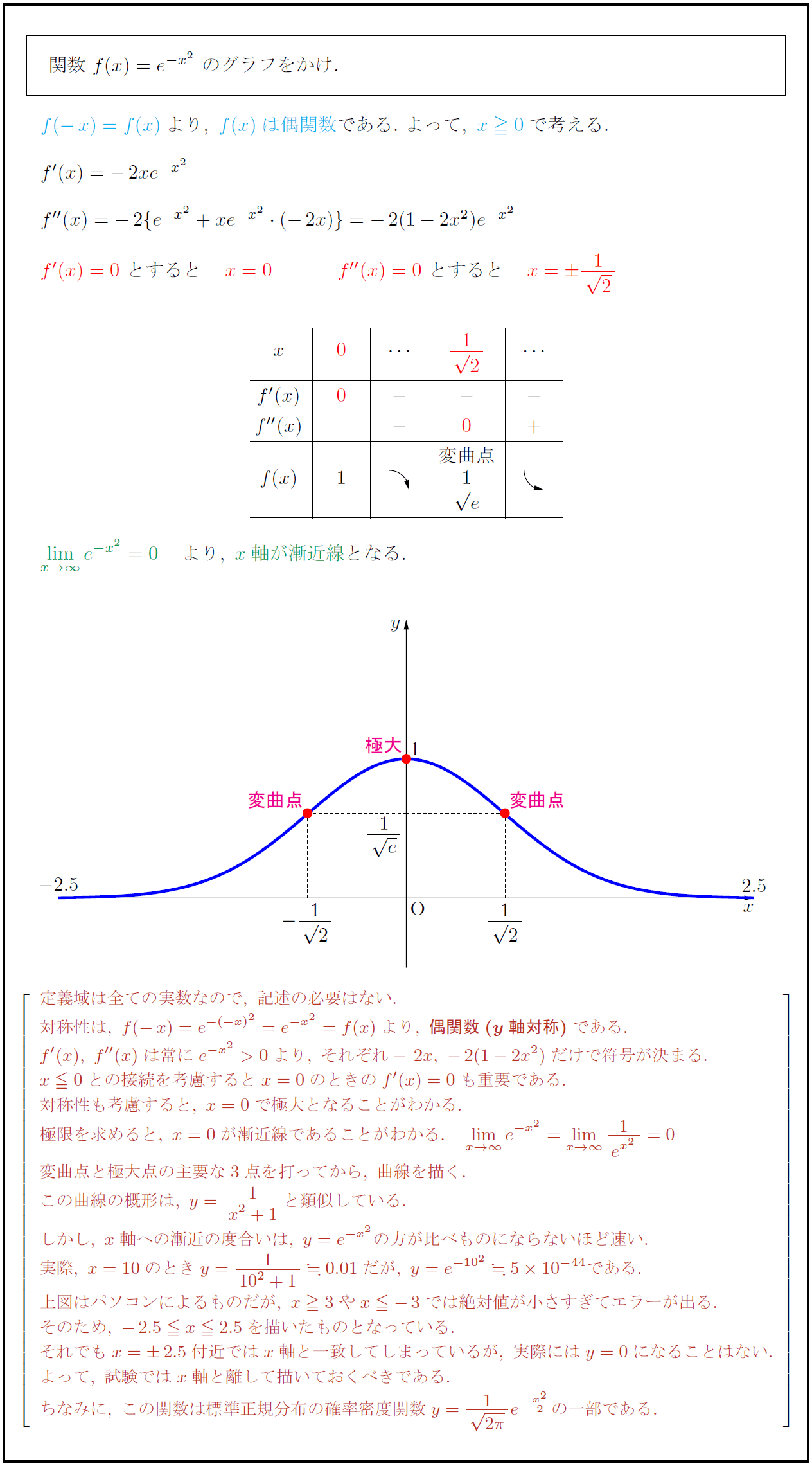
定義域は全ての実数なので,\ 記述の必要はない. 対称性は,\ f(-x)=e^{-(-x)²}=e^{-x²}=f(x)より,\ {偶関数(y軸対称)}である. f'(x),\ f”(x)は常にe^{-x²}>0より,\ それぞれ-2x,\ -2(1-2x²)だけで符号が決まる. x0との接続を考慮するとx=0のときのf'(x)=0も重要である. 対称性も考慮すると,\ x=0で極大となることがわかる. 極限を求めると,\ x=0が漸近線であることがわかる. lim[x→∞]e^{-x²}=lim[x→∞]{1}{e^{x²=0 変曲点と極大点の主要な3点を打ってから,\ 曲線を描く. この曲線の概形は,\ y={1}{x²+1}と類似している. しかし,\ x軸への漸近の度合いは,\ y=e^{-x²}の方が比べものにならないほど速い. 実際,\ x=10のときy={1}{10²+1}0.01だが,\ y=e^{-10²}510^{-44}である. 上図はパソコンによるものだが,\ x3やx-3では絶対値が小さすぎてエラーが出る. そのため,\ -2.5 x2.5を描いたものとなっている. それでもx=2.5付近ではx軸と一致してしまっているが,\ 実際にはy=0になることはない. よって,\ 試験ではx軸と離して描いておくべきである. ちなみに,\ この関数は標準正規分布の確率密度関数y={1}2πe^{-x²}{2の一部である.

