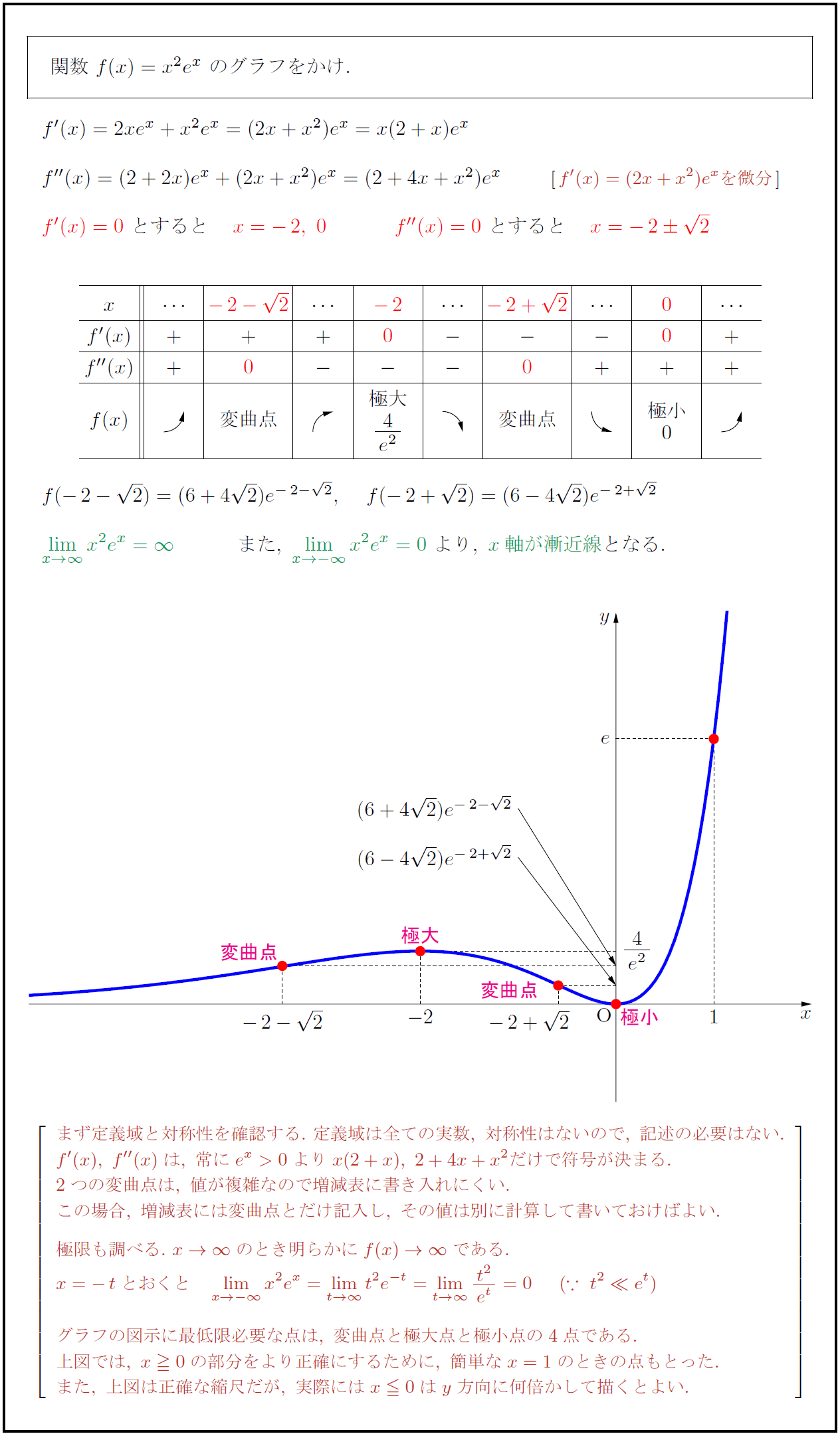
まず定義域と対称性を確認する.\ 定義域は全ての実数,\ 対称性はないので,\ 記述の必要はない. f'(x),\ f”(x)は,\ 常にe^x>0よりx(2+x),\ 2+4x+x²だけで符号が決まる. 2つの変曲点は,\ 値が複雑なので増減表に書き入れにくい. この場合,\ 増減表には変曲点とだけ記入し,\ その値は別に計算して書いておけばよい. 極限も調べる.\ x→∞ のとき明らかにf(x)→∞ である. x=-tとおくと limx→-∞}x²e^x=limt→∞}t²e^{-t}=limt→∞}{t²}{e^t}=0 (∵\ t²\ll e^t) グラフの図示に最低限必要な点は,\ 変曲点と極大点と極小点の4点である. 上図では,\ x0の部分をより正確にするために,\ 簡単なx=1のときの点もとった. また,\ 上図は正確な縮尺だが,\ 実際にはx0はy方向に何倍かして描くとよい.

